We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We consider the fractional critical problem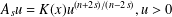 
$A_{s}u=K(x)u^{(n+2s)/(n-2s)},u>0$ in 
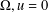$\unicode[STIX]{x1D6FA},u=0$ on 
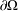$\unicode[STIX]{x2202}\unicode[STIX]{x1D6FA}$, where 
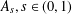$A_{s},s\in (0,1)$, is the fractional Laplace operator and 
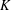$K$ is a given function on a bounded domain 
$\unicode[STIX]{x1D6FA}$ of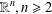 
$\mathbb{R}^{n},n\geq 2$. This is based on A. Bahri’s theory of critical points at infinity in Bahri [Critical Points at Infinity in Some Variational Problems, Pitman Research Notes in Mathematics Series, 182 (Longman Scientific & Technical, Harlow, 1989)]. We prove Bahri’s estimates in the fractional setting and we provide existence theorems for the problem when 
$K$ is close to 1.
