The purpose of this note is to focus on the finiteness of the weighted likelihood estimator (WLE) of ability in the context of dichotomous and polytomous item response theory (IRT) models. It is established that the WLE always returns finite ability estimates. This general result is valid for dichotomous (one-, two-, three- and four-parameter logistic) IRT models, the class of polytomous difference models and divide-by-total models, independently of the number of items, the item parameters and the response patterns. Further implications of this result are outlined.

The prescriptive infinitive can be found in the North Germanic languages, is very old, and yet is largely unnoticed and undescribed. It is used in a very limited pragmatic context of a pleasant atmosphere by adults towards very young children, or towards pets or (more rarely) adults. It has a set of syntactic properties that distinguishes it from the imperative: Negation is pre-verbal, subjects are pre-verbal, subjects are third person and are only expressed by lexical DPs, not personal pronouns. It can be found in modern child language corpora, but probably originated before ad 500. The paper is largely descriptive, but some theoretical solutions to the puzzles of this construction are proposed.

This paper proves two results on the field of rationality $\mathbb{Q}({\it\pi})$ for an automorphic representation ${\it\pi}$, which is the subfield of $\mathbb{C}$ fixed under the subgroup of $\text{Aut}(\mathbb{C})$ stabilizing the isomorphism class of the finite part of ${\it\pi}$. For general linear groups and classical groups, our first main result is the finiteness of the set of discrete automorphic representations ${\it\pi}$ such that ${\it\pi}$ is unramified away from a fixed finite set of places, ${\it\pi}_{\infty }$ has a fixed infinitesimal character, and $[\mathbb{Q}({\it\pi}):\mathbb{Q}]$ is bounded. The second main result is that for classical groups, $[\mathbb{Q}({\it\pi}):\mathbb{Q}]$ grows to infinity in a family of automorphic representations in level aspect whose infinite components are discrete series in a fixed $L$-packet under mild conditions.

Let $\mathcal S$ be a Serre subcategory of the category of 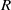$R$-modules, where $R$ is a commutative Noetherian ring. Let $\mathfrak a$ and $\mathfrak b$ be ideals of 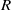$R$ and let 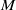$M$ and 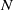$N$ be finite $R$-modules. We prove that if 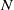$N$ and 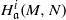$H^i_{\mathfrak a}(M,N)$ belong to 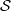$\mathcal S$ for all 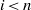$i\lt n$ and if 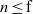$n\leq \mathrm {f}$-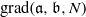$\mathrm {grad}({\mathfrak a},{\mathfrak b},N )$, then 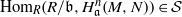$\mathrm {Hom}_{R}(R/{\mathfrak b},H^n_{{\mathfrak a}}(M,N))\in \mathcal S$. We deduce that if either $H^i_{\mathfrak a}(M,N)$ is finite or 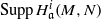$\mathrm {Supp}\,H^i_{\mathfrak a}(M,N)$ is finite for all $i\lt n$, then $\mathrm {Ass}\,H^n_{\mathfrak a}(M,N)$ is finite. Next we give an affirmative answer, in certain cases, to the following question. If, for each prime ideal 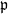${\mathfrak {p}}$ of $R$, there exists an integer 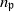$n_{\mathfrak {p}}$ such that 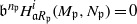$\mathfrak b^{n_{\mathfrak {p}}} H^i_{\mathfrak a R_{\mathfrak {p}}}({M_{\mathfrak {p}}},{N_{\mathfrak {p}}})=0$ for every 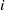$i$ less than a fixed integer $t$, then does there exist an integer $n$ such that $\mathfrak b^nH^i_{\mathfrak a}(M,N)=0$ for all 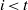$i\lt t$? A formulation of this question is referred to as the local-global principle for the annihilation of generalised local cohomology modules. Finally, we prove that there are local-global principles for the finiteness and Artinianness of generalised local cohomology modules.

The Extended Projection Principle (EPP) has remained a controversial topic in generative grammar. This article proposes to derive the EPP from a generalized theory of nominal case and verbal agreement. According to the proposal presented in this article, morphosyntactic features such as case and verbal phi-features are valued uniformly by the closest asymmetrically c-commanding element, whereas the PF interface is constrained so as to prevent verbs from being valued nominal case and nominals by verbal phi-features. This constraint together with a new theory of valuation explains the appearance of the EPP. The theory is applied to the investigation of negative clauses in Finnish and other languages, Finnish (elliptical) non-finite negative clauses, expletive constructions, multiple wh-movement in a variety of languages, multiple agreement both in the finite and nominal domains, and asymmetries between finite and non-finite clauses.