We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
Let G be a compact connected Lie group, and let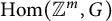 
$\operatorname {Hom}({\mathbb {Z}}^m,G)$ be the space of pairwise commuting m-tuples in G. We study the problem of which primes 
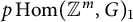$p \operatorname {Hom}({\mathbb {Z}}^m,G)_1$, the connected component of 
$\operatorname {Hom}({\mathbb {Z}}^m,G)$ containing the element 
$(1,\ldots ,1)$, has p-torsion in homology. We will prove that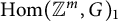 
$\operatorname {Hom}({\mathbb {Z}}^m,G)_1$ for 
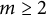$m\ge 2$ has p-torsion in homology if and only if p divides the order of the Weyl group of G for 
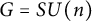$G=SU(n)$ and some exceptional groups. We will also compute the top homology of 
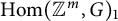$\operatorname {Hom}({\mathbb {Z}}^m,G)_1$ and show that 
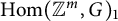$\operatorname {Hom}({\mathbb {Z}}^m,G)_1$ always has 2-torsion in homology whenever G is simply-connected and simple. Our computation is based on a new homotopy decomposition of 
$\operatorname {Hom}({\mathbb {Z}}^m,G)_1$, which is of independent interest and enables us to connect torsion in homology to the combinatorics of the Weyl group.
