We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
Existence of specific eternal solutions in exponential self-similar form to the following quasilinear diffusion equation with strong absorption\[ \partial_t u=\Delta u^m-|x|^{\sigma}u^q, \]posed for $(t,\,x)\in (0,\,\infty )\times \mathbb {R}^N$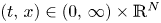
, with $m>1$
, $q\in (0,\,1)$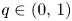
and $\sigma =\sigma _c:=2(1-q)/ (m-1)$
is proved. Looking for radially symmetric solutions of the form\[ u(t,x)={\rm e}^{-\alpha t}f(|x|\,{\rm e}^{\beta t}), \quad \alpha=\frac{2}{m-1}\beta, \]we show that there exists a unique exponent $\beta ^*\in (0,\,\infty )$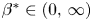
for which there exists a one-parameter family $(u_A)_{A>0}$
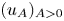of solutions with compactly supported and non-increasing profiles $(f_A)_{A>0}$
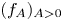satisfying $f_A(0)=A$
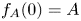and $f_A'(0)=0$
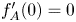. An important feature of these solutions is that they are bounded and do not vanish in finite time, a phenomenon which is known to take place for all non-negative bounded solutions when $\sigma \in (0,\,\sigma _c)$
.
