It is known that hyperbolic linear delay difference equations are shadowable on the half-line. In this article, we prove the converse and hence the equivalence between hyperbolicity and the positive shadowing property for the following two classes of linear delay difference equations: (a) for non-autonomous equations with finite delays and uniformly bounded compact coefficient operators in Banach spaces and (b) for Volterra difference equations with infinite delay in finite dimensional spaces.

For linear differential systems, the Sacker–Sell spectrum (dichotomy spectrum) and the contractible set are the same. However, we claim that this is not true for the linear difference equations. A counterexample is given. For the convenience of research, we study the relations between the dichotomy spectrum and the contractible set under the framework on time scales. In fact, by a counterexample, we show that the contractible set could be different from dichotomy spectrum on time scales established by Siegmund [J. Comput. Appl. Math., 2002]. Furthermore, we find that there is no bijection between them. In particular, for the linear difference equations, the contractible set is not equal to the dichotomy spectrum. To counter this mismatch, we propose a new notion called generalized contractible set and we prove that the generalized contractible set is exactly the dichotomy spectrum. Our approach is based on roughness theory and Perron's transformation. In this paper, a new method for roughness theory on time scales is provided. Moreover, we provide a time-scaled version of the Perron's transformation. However, the standard argument is invalid for Perron's transformation. Thus, some novel techniques should be employed to deal with this problem. Finally, an example is given to verify the theoretical results.

In this paper, we extend to the non-Hille–Yosida case a variation of constants formula for a nonautonomous and nonhomogeneous Cauchy problems first obtained by Gühring and Räbiger. By using this variation of constants formula, we derive a necessary and sufficient condition for the existence of an exponential dichotomy for the evolution family generated by the associated nonautonomous homogeneous problem. We also prove a persistence result of the exponential dichotomy for small perturbations. Finally, we illustrate our results by considering two examples. The first example is a parabolic equation with nonlocal and nonautonomous boundary conditions, and the second example is an age-structured model that is a hyperbolic equation.

In this article we study exponential trichotomy for infinite dimensional discrete time dynamical systems. The goal of this article is to prove that finite time exponential trichotomy conditions allow us to derive exponential trichotomy for arbitrary times. We present an application to the case of pseudo orbits in some neighborhood of a normally hyperbolic set.

We consider the quasi-periodic solutions bifurcated from a degenerate homoclinic solution. Assume that the unperturbed system has a homoclinic solution and a hyperbolic fixed point. The bifurcation function for the existence of a quasi-periodic solution of the perturbed system is obtained by functional analysis methods. The zeros of the bifurcation function correspond to the existence of the quasi-periodic solution at the non-zero parameter values. Some solvable conditions of the bifurcation equations are investigated. Two examples are given to illustrate the results.

By applying the theory of exponential dichotomies and contraction mapping, we establish some existence and uniqueness results for weighted pseudo almost periodic solutions of some differential equations with piecewise constant arguments. For this purpose, we also describe some basic properties of weighted pseudo almost periodic sequences.

Using the method of exponential dichotomies, we establish a new existence and uniqueness theorem for almost automorphic solutions of differential equations with piecewise constant argument of the form

$$\begin{eqnarray*}{x}^{\prime } (t)= A(t)x(t)+ B(t)x(\lfloor t\rfloor )+ f(t), \quad t\in \mathbb{R} ,\end{eqnarray*}$$

$\lfloor \cdot \rfloor $

$A(t), B(t): \mathbb{R} \rightarrow { \mathbb{R} }^{q\times q} $

$f(t): \mathbb{R} \rightarrow { \mathbb{R} }^{q} $

We establish a discrete-time criteria guaranteeing the existence of an exponential dichotomy in the continuous-time behavior of an abstract evolution family. We prove that an evolution family 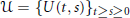$\mathcal{U}\,=\,{{\{U(t,\,s)\}}_{t\ge s\ge 0}}$ acting on a Banach space $X$ is uniformly exponentially dichotomic (with respect to its continuous-time behavior) if and only if the corresponding difference equation with the inhomogeneous term from a vector-valued Orlicz sequence space 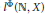${{l}^{\Phi }}(\mathbb{N},\,X)$ admits a solution in the same 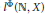${{l}^{\Phi }}(\mathbb{N},\,X)$. The technique of proof effectively eliminates the continuity hypothesis on the evolution family (i.e., we do not assume that $U(\,\cdot \,,\,s)x$ or 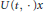$U(t,\,\cdot \,)x$ is continuous on $[s,\,\infty )$, and respectively $[0,\,t])$. Thus, some known results given by Coffman and Schaffer, Perron, and Ta Li are extended.