We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We study analytic properties function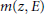 
$m\left( z,\,E \right)$, which is defined on the upper half-plane as an integral from the shifted 
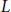$L$-function of an elliptic curve. We show that 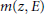$m\left( z,\,E \right)$ analytically continues to a meromorphic function on the whole complex plane and satisfies certain functional equation. Moreover, we give explicit formula for 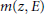$m\left( z,\,E \right)$ in the strip 
$\left| \Im z \right|\,<\,2\pi$.
