We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
Let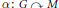 
$\alpha :\,G\,\curvearrowright \,M$ be a spatial action of a countable abelian group on a “spatial” von Neumann algebra 
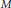$M$ and let 
$S$ be its unital subsemigroup with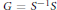 
$G\,=\,{{S}^{-1}}S$. We explicitly compute the essential commutant and the essential fixed-points, modulo the Schatten 
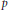$p$-class or the compact operators, of the 
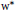${{w}^{*}}$-semicrossed product of 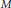$M$ by $S$ when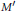 
${{M}^{'}}$ contains no non-zero compact operators. We also prove a weaker result when 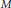$M$ is a von Neumann algebra on a finite dimensional Hilbert space and 
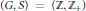$\left( G,\,S \right)\,=\,\left( \mathbb{Z},\,{{\mathbb{Z}}_{+}} \right)$, which extends a famous result due to Davidson (1977) for the classical analytic Toeplitz operators.
