This paper studies Auslander-Reiten triangles in subcategories of triangulated categories. The main theorem shows that the Auslander-Reiten triangles in a subcategory are closely connected with the approximation properties of the subcategory. Namely, let C be an object in the subcategory C of the triangulated category T, and let

be an Auslander-Reiten triangle in T. Then under suitable assumptions, there is an Auslander-Reiten triangle

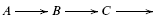
in C if and only if there is a minimal right-C-approximation of the form

.

The theory is used to give a new proof of the existence of Auslander-Reiten sequences over finite dimensional algebras.

In order to construct a counterexample to Zilber's conjecture—that a strongly minimal set has a degenerate, affine or field-like geometry—Ehud Hrushovski invented an amalgamation technique which has yielded all the exotic geometries so far. We shall present a framework for this construction in the language of standard geometric stability and show how some of the recent constructions fit into this setting. We also ask some fundamental questions concerning this method.

For homogeneous, two-dimensional random field ξ(t), t ∈ R2 we develop the ‘half' spectral theory sufficient to rigorously define its envelope η (t). We then specialise to the case of ξ Gaussian, which implies η is Rayleigh, and consider the mean value of a certain characteristic of the sets {t:η(t) ≧ u} (u ≧ 0). From this we deduce some qualitative information about the sample path behaviour of the Rayleigh field η .