We show that robustly transitive endomorphisms of a closed manifold must have a non-trivial dominated splitting or be a local diffeomorphism. This allows to get some topological obstructions for the existence of robustly transitive endomorphisms. To obtain the result, we must understand the structure of the kernel of the differential and the recurrence to the critical set of the endomorphism after perturbation.

The Dixmier Conjecture says that every endomorphism of the (first) Weyl algebra $A_{1}$ (over a field of characteristic zero) is an automorphism, i.e., if $PQ-QP=1$ for some $P,Q\in A_{1}$, then $A_{1}=K\langle P,Q\rangle$. The Weyl algebra $A_{1}$ is a $\mathbb{Z}$-graded algebra. We prove that the Dixmier Conjecture holds if the elements $P$ and $Q$ are sums of no more than two homogeneous elements of $A_{1}$ (there is no restriction on the total degrees of $P$ and $Q$).

This paper studies the growths of endomorphisms of finitely generated semigroups. The growth is a certain dynamical characteristic describing how iterations of the endomorphism ‘stretch’ balls in the Cayley graph of the semigroup. We make a detailed study of the relation of the growth of an endomorphism of a finitely generated semigroup and the growth of the restrictions of the endomorphism to finitely generated invariant subsemigroups. We also study the possible values endomorphism growths can attain. We show the role of linear algebra in calculating the growths of endomorphisms of homogeneous semigroups. Proofs are a mixture of syntactic algebraic rewriting techniques and analytical tricks. We state various problems and suggestions for future research.

Suppose that ${\Gamma }^{+ } $ is the positive cone of a totally ordered abelian group $\Gamma $, and $(A, {\Gamma }^{+ } , \alpha )$ is a system consisting of a ${C}^{\ast } $-algebra $A$, an action $\alpha $ of ${\Gamma }^{+ } $ by extendible endomorphisms of $A$. We prove that the partial-isometric crossed product $A\hspace{0.167em} { \mathop{\times }\nolimits}_{\alpha }^{\mathrm{piso} } \hspace{0.167em} {\Gamma }^{+ } $ is a full corner in the subalgebra of $\L ({\ell }^{2} ({\Gamma }^{+ } , A))$, and that if $\alpha $ is an action by automorphisms of $A$, then it is the isometric crossed product $({B}_{{\Gamma }^{+ } } \otimes A)\hspace{0.167em} {\mathop{\times }\nolimits }^{\mathrm{iso} } \hspace{0.167em} {\Gamma }^{+ } $, which is therefore a full corner in the usual crossed product of system by a group of automorphisms. We use these realizations to identify the ideal of $A\hspace{0.167em} { \mathop{\times }\nolimits}_{\alpha }^{\mathrm{piso} } \hspace{0.167em} {\Gamma }^{+ } $ such that the quotient is the isometric crossed product $A\hspace{0.167em} { \mathop{\times }\nolimits}_{\alpha }^{\mathrm{iso} } \hspace{0.167em} {\Gamma }^{+ } $.

The automorphisms of the canonical core UHF subalgebra ℱn of the Cuntz algebra 𝒪n do not necessarily extend to automorphisms of 𝒪n. Simple examples are discussed within the family of infinite tensor products of (inner) automorphisms of the matrix algebras Mn. In that case, necessary and sufficient conditions for the extension property are presented. Also addressed is the problem of extending to 𝒪n the automorphisms of the diagonal 𝒟n, which is a regular maximal abelian subalgebra with Cantor spectrum. In particular, it is shown that there exist product-type automorphisms of 𝒟n that do not extend to (possibly proper) endomorphisms of 𝒪n.

We completely determine the localized automorphisms of the Cuntz algebras corresponding to permutation matrices in Mn ⊗ Mn for n = 3 and n = 4. This result is obtained through a combination of general combinatorial techniques and large scale computer calculations. Our analysis proceeds according to the general scheme proposed in a previous paper, where we analysed in detail the case of using labelled rooted trees. We also discuss those proper endomorphisms of these Cuntz algebras which restrict to automorphisms of their respective diagonals. In the case of we compute the number of automorphisms of the diagonal induced by permutation matrices in M3 ⊗ M3 ⊗ M3.

Let $G$ be a compact topological group and let 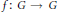$f:\,G\,\to \,G$ be a continuous transformation of $G$. Define 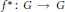${{f}^{*}}:G\to G$ by 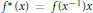${{f}^{*}}\left( x \right)\,=\,f\left( {{x}^{-1}} \right)x$ and let 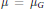$\mu \,=\,{{\mu }_{G}}$ be Haar measure on $G$. Assume that 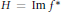$H\,=\,\text{IM}\,{{f}^{*}}$ is a subgroup of $G$ and for every measurable 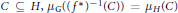$C\,\subseteq \,H,\,{{\mu }_{G}}{{\left( \left( {{f}^{*}} \right) \right)}^{-1}}\left( \left( C \right) \right)\,=\,\mu H\left( C \right)$. Then for every measurable 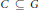$C\,\subseteq \,G$, there exist 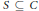$S\subseteq C$ and 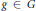$g\,\in \,G$ such that 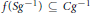$f\left( S{{g}^{-1}} \right)\,\subseteq \,C{{g}^{-1}}$ and 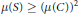$\mu \left( S \right)\,\ge \,{{\left( \mu \left( C \right) \right)}^{2}}$.

For a set $X$ and a variety $\mathcal{V}$ of bands, let $B_{\mathcal{V}}(X)$ be the relatively free band in $\mathcal{V}$ on $X$. For an arbitrary band variety $\mathcal{V}$ and an arbitrary set $X$, we determine the group of automorphisms of $\mathrm{End}(B_{\mathcal{V}}(X))$, the monoid of endomorphisms of $B_{\mathcal{V}}(X)$.