The minimum roman dominating problem (denoted by γR(G), the weight of minimum roman dominating function of graph G) is a variant of the very well known minimum dominating set problem (denoted by γ(G), the cardinality of minimum dominating set of graph G). Both problems remain NP-Complete when restricted to P5-free graph class [A.A. Bertossi, Inf. Process. Lett. 19 (1984) 37–40; E.J. Cockayne, et al. Discret. Math. 278 (2004) 11–22]. In this paper we study both problems restricted to some subclasses of P5-free graphs. We describe robust algorithms that solve both problems restricted to (P5,(s,t)-net)-free graphs in polynomial time. This result generalizes previous works for both problems, and improves existing algorithms when restricted to certain families such as (P5,bull)-free graphs. It turns out that the same approach also serves to solve problems for general graphs in polynomial time whenever γ(G) and γR(G) are fixed (more efficiently than naive algorithms). Moreover, the algorithms described are extremely simple which makes them useful for practical purposes, and as we show in the last section it allows to simplify algorithms for significant classes such as cographs.

Let 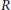$R$ be a commutative ring with 1. In a 1995 paper in J. Algebra, Sharma and Bhatwadekar defined a graph on 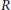$R$, 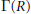$\Gamma \left( R \right)$, with vertices as elements of 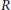$R$, where two distinct vertices $a$ and 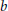$b$ are adjacent if and only if 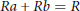$Ra\,+\,Rb\,=\,R$. In this paper, we consider a subgraph 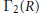${{\Gamma }_{2}}\left( R \right)$ of 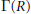$\Gamma \left( R \right)$ that consists of non-unit elements. We investigate the behavior of 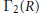${{\Gamma }_{2}}\left( R \right)$ and 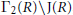${{\Gamma }_{2}}\left( R \right)\backslash \text{J}\left( R \right)$, where 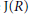$\text{J}\left( R \right)$ is the Jacobson radical of 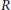$R$. We associate the ring properties of 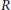$R$, the graph properties of 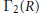${{\Gamma }_{2}}\left( R \right)$, and the topological properties of 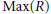$\text{Max}\left( R \right)$. Diameter, girth, cycles and dominating sets are investigated, and algebraic and topological characterizations are given for graphical properties of these graphs.

Let D be the punctured unit disk. It is easy to see that no pair x, y in D can cover D in the sense that D cannot be contained in the union of the unit disks centred at x and y. With this fact in mind, let Vn = {X1, X2, …, Xn}, where X1, X2, … are random points sampled independently from a uniform distribution on D. We prove that, with asymptotic probability 1, there exist two points in Vn that cover all of Vn.