We introduce and study Dirichlet-type spaces 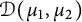$\mathcal D(\mu _1, \mu _2)$ of the unit bidisc 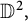$\mathbb D^2,$ where 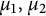$\mu _1, \mu _2$ are finite positive Borel measures on the unit circle. We show that the coordinate functions 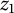$z_1$ and $z_2$ are multipliers for $\mathcal D(\mu _1, \mu _2)$ and the complex polynomials are dense in 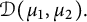$\mathcal D(\mu _1, \mu _2).$ Further, we obtain the division property and solve Gleason’s problem for 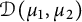$\mathcal D(\mu _1, \mu _2)$ over a bidisc centered at the origin. In particular, we show that the commuting pair 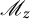$\mathscr M_z$ of the multiplication operators $\mathscr M_{z_1}, \mathscr M_{z_2}$ on 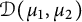$\mathcal D(\mu _1, \mu _2)$ defines a cyclic toral 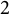$2$-isometry and 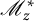$\mathscr M^*_z$ belongs to the Cowen–Douglas class 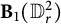$\mathbf {B}_1(\mathbb D^2_r)$ for some 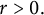$r>0.$ Moreover, we formulate a notion of wandering subspace for commuting tuples and use it to obtain a bidisc analog of Richter’s representation theorem for cyclic analytic $2$-isometries. In particular, we show that a cyclic analytic toral 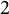$2$-isometric pair T with cyclic vector $f_0$ is unitarily equivalent to $\mathscr M_z$ on $\mathcal D(\mu _1, \mu _2)$ for some 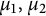$\mu _1,\mu _2$ if and only if 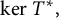$\ker T^*,$ spanned by 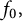$f_0,$ is a wandering subspace for 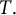$T.$