We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We expose different methods of regularizations of subsolutions in the context of discrete weak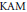 
$\text{KAM}$ theory that allow us to prove the existence and the density of 
${{C}^{1,1}}$ subsolutions. Moreover, these subsolutions can be made strict and smooth outside of the Aubry set.
