We present the convergence analysis of locally divergence-free discontinuous Galerkin methodsfor the induction equations which appear in the ideal magnetohydrodynamic system. When we use a second order Runge Kutta time discretization, under the CFL condition $\Delta t\sim h^{4/3}$ 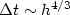 , we obtain error estimates in L 2 of order $\mathcal{O} (\Delta t^2 + h^{m + 1/2})$
, we obtain error estimates in L 2 of order $\mathcal{O} (\Delta t^2 + h^{m + 1/2})$ 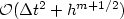 where m is the degree of the local polynomials.
where m is the degree of the local polynomials.