We consider classes 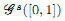 of subsets of [0, 1], originally introduced by Falconer, that are closed under countable intersections, and such that every set in the class has Hausdorff dimension at least s. We provide a Frostman-type lemma to determine if a limsup set is in such a class. Suppose that E = lim sup En ⊂ [0, 1], and that μn are probability measures with support in En. If there exists a constant C such that
of subsets of [0, 1], originally introduced by Falconer, that are closed under countable intersections, and such that every set in the class has Hausdorff dimension at least s. We provide a Frostman-type lemma to determine if a limsup set is in such a class. Suppose that E = lim sup En ⊂ [0, 1], and that μn are probability measures with support in En. If there exists a constant C such that
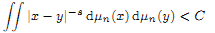
for all n, then, under suitable conditions on the limit measure of the sequence (μn), we prove that the set E is in the class 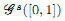 .
.
As an application we prove that, for α > 1 and almost all λ ∈ (½, 1), the set
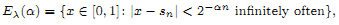
where 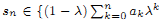 and ak ∈ {0, 1}}, belongs to the class
and ak ∈ {0, 1}}, belongs to the class 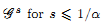 . This improves one of our previously published results.
. This improves one of our previously published results.
 $\text{SL}(n+1,\mathbb{Z})\backslash \text{SL}(n+1,\mathbb{R})$ and applications
$\text{SL}(n+1,\mathbb{Z})\backslash \text{SL}(n+1,\mathbb{R})$ and applications
 $p$-adic Littlewood conjecture
$p$-adic Littlewood conjecture