We study the symplectic geometry of derived intersections of Lagrangian morphisms. In particular, we show that for a functional $f : X \rightarrow \mathbb {A}_{k}^{1}$, the derived critical locus has a natural Lagrangian fibration $\textbf {Crit}(f) \rightarrow X$. In the case where f is nondegenerate and the strict critical locus is smooth, we show that the Lagrangian fibration on the derived critical locus is determined by the Hessian quadratic form.

In this short paper, we combine the representability theorem introduced in [Porta and Yu, Representability theorem in derived analytic geometry, preprint, 2017, arXiv:1704.01683; Porta and Yu, Derived Hom spaces in rigid analytic geometry, preprint, 2018, arXiv:1801.07730] with the theory of derived formal models introduced in [António, $p$-adic derived formal geometry and derived Raynaud localization theorem, preprint, 2018, arXiv:1805.03302] to prove the existence representability of the derived Hilbert space 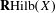$\mathbf{R}\text{Hilb}(X)$ for a separated 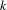$k$-analytic space 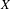$X$. Such representability results rely on a localization theorem stating that if 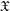$\mathfrak{X}$ is a quasi-compact and quasi-separated formal scheme, then the $\infty$-category 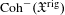$\text{Coh}^{-}(\mathfrak{X}^{\text{rig}})$ of almost perfect complexes over the generic fiber can be realized as a Verdier quotient of the 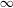$\infty$-category 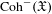$\text{Coh}^{-}(\mathfrak{X})$. Along the way, we prove several results concerning the 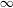$\infty$-categories of formal models for almost perfect modules on derived 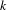$k$-analytic spaces.

In this paper, we relate Lie algebroids to Costello’s version of derived geometry. For instance, we show that each Lie algebroid – and the natural generalization to dg Lie algebroids – provides an (essentially unique) $L_{\infty }$ space. More precisely, we construct a faithful functor from the category of Lie algebroids to the category of $L_{\infty }$ spaces. Then we show that for each Lie algebroid $L$, there is a fully faithful functor from the category of representations up to homotopy of $L$ to the category of vector bundles over the associated $L_{\infty }$ space. Indeed, this functor sends the adjoint complex of $L$ to the tangent bundle of the $L_{\infty }$ space. Finally, we show that a shifted symplectic structure on a dg Lie algebroid produces a shifted symplectic structure on the associated $L_{\infty }$ space.