We prove that if A is the infinitesimal generator of a bounded analytic semigroup in a sector {z ∊ C : |arg z| ≦ (απ)/2} of bounded linear operators on a Banach space, then the following inequalities hold:
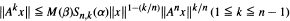
for any x ∊ D(An) and for any 0 < β < α. This result helps us to answer in affirmative a question raised by M. W. Certain and T. G. Kurtz [3]. Similar inequalities are proved for cosine operator funtions.