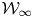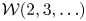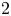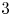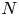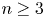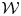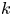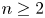1 results
Universal two-parameter 𝒲∞-algebra and vertex algebras of type 𝒲(2, 3, …, N)
- Part of
-
- Journal:
- Compositio Mathematica / Volume 157 / Issue 1 / January 2021
- Published online by Cambridge University Press:
- 10 February 2021, pp. 12-82
- Print publication:
- January 2021
-
- Article
- Export citation
-
We prove the longstanding physics conjecture that there exists a unique two-parameter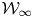
${\mathcal {W}}_{\infty }$-algebra which is freely generated of type 
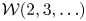${\mathcal {W}}(2,3,\ldots )$, and generated by the weights 
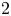$2$ and 
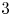$3$ fields. Subject to some mild constraints, all vertex algebras of type 
${\mathcal {W}}(2,3,\ldots , N)$ for some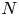 
$N$ can be obtained as quotients of this universal algebra. As an application, we show that for 
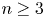$n\geq 3$, the structure constants for the principal 
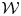${\mathcal {W}}$-algebras 
${\mathcal {W}}^k({\mathfrak s}{\mathfrak l}_n, f_{\text {prin}})$ are rational functions of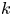 
$k$ and 
$n$, and we classify all coincidences among the simple quotients 
${\mathcal {W}}_k({\mathfrak s}{\mathfrak l}_n, f_{\text {prin}})$ for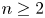 
$n\geq 2$. We also obtain many new coincidences between 
${\mathcal {W}}_k({\mathfrak s}{\mathfrak l}_n, f_{\text {prin}})$ and other vertex algebras of type 
${\mathcal {W}}(2,3,\ldots , N)$ which arise as cosets of affine vertex algebras or nonprincipal 
${\mathcal {W}}$-algebras.
