We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
Let A and G be finite groups and suppose that A acts via automorphisms on G with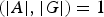 
$(|A|, |G|)=1$. We study how certain conditions on the Sylow 2-subgroups of the fixed point subgroup of the action 
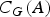$C_G(A)$ may imply the non-simplicity or solubility of G.
