We show that under mild conditions, the connected sum $M\# N$ of simply connected, closed, orientable n-dimensional Poincaré Duality complexes M and N is hyperbolic and has no homotopy exponent at all but finitely many primes, verifying a weak version of Moore’s conjecture. This is derived from an elementary framework involving $CW$-complexes satisfying certain conditions.

Let $X$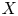 and $Y$ 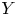be oriented topological manifolds of dimension $n\!+\!2$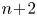, and let $K\! \subset \! X$ 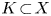and $J \! \subset \! Y$ 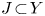be connected, locally-flat, oriented, $n$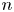–dimensional submanifolds. We show that up to orientation preserving homeomorphism there is a well-defined connected sum $(X,K)\! \mathbin {\#}\! (Y,J)$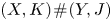. For $n = 1$, the proof is classical, relying on results of Rado and Moise. For dimensions $n=3$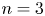 and $n \ge 6$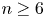, results of Edwards-Kirby, Kirby, and Kirby-Siebenmann concerning higher dimensional topological manifolds are required. For $n = 2, 4,$ 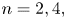and $5$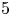, Freedman and Quinn's work on topological four-manifolds is required along with the higher dimensional theory.

We explore the constraints imposed by Poincaré duality on the resonance varieties of a graded algebra. For a three-dimensional Poincaré duality algebra A, we obtain a fairly precise geometric description of the resonance varieties ${\cal R}^i_k(A)$.