The classical model for studying one-phase Hele-Shaw flows is based on a highly nonlinear moving boundary problem with the fluid velocity related to pressure gradients via a Darcy-type law. In a standard configuration with the Hele-Shaw cell made up of two flat stationary plates, the pressure is harmonic. Therefore, conformal mapping techniques and boundary integral methods can be readily applied to study the key interfacial dynamics, including the Saffman–Taylor instability and viscous fingering patterns. As well as providing a brief review of these key issues, we present a flexible numerical scheme for studying both the standard and nonstandard Hele-Shaw flows. Our method consists of using a modified finite-difference stencil in conjunction with the level-set method to solve the governing equation for pressure on complicated domains and track the location of the moving boundary. Simulations show that our method is capable of reproducing the distinctive morphological features of the Saffman–Taylor instability on a uniform computational grid. By making straightforward adjustments, we show how our scheme can easily be adapted to solve for a wide variety of nonstandard configurations, including cases where the gap between the plates is linearly tapered, the plates are separated in time, and the entire Hele-Shaw cell is rotated at a given angular velocity.

We prove that for $0<p<+\infty $ and $-1<\alpha <+\infty ,$ a conformal map defined on the unit disk belongs to the weighted Bergman space $A_{\alpha }^p$ if and only if a certain integral involving the hyperbolic distance converges.

Let 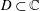$D\subset \mathbb{C}$ be a domain with 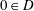$0\in D$. For $R>0$, let 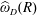$\widehat{\unicode[STIX]{x1D714}}_{D}(R)$ denote the harmonic measure of 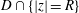$D\cap \{|z|=R\}$ at 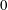$0$ with respect to the domain 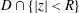$D\cap \{|z|<R\}$ and let 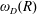$\unicode[STIX]{x1D714}_{D}(R)$ denote the harmonic measure of 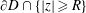$\unicode[STIX]{x2202}D\cap \{|z|\geqslant R\}$ at $0$ with respect to 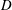$D$. The behavior of the functions $\unicode[STIX]{x1D714}_{D}$ and 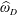$\widehat{\unicode[STIX]{x1D714}}_{D}$ near $\infty$ determines (in some sense) how large $D$ is. However, it is not known whether the functions $\unicode[STIX]{x1D714}_{D}$ and 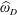$\widehat{\unicode[STIX]{x1D714}}_{D}$ always have the same behavior when 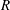$R$ tends to 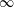$\infty$. Obviously, 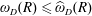$\unicode[STIX]{x1D714}_{D}(R)\leqslant \widehat{\unicode[STIX]{x1D714}}_{D}(R)$ for every $R>0$. Thus, the arising question, first posed by Betsakos, is the following: Does there exist a positive constant 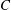$C$ such that for all simply connected domains $D$ with $0\in D$ and all 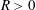$R>0$,

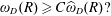$$\begin{eqnarray}\unicode[STIX]{x1D714}_{D}(R)\geqslant C\widehat{\unicode[STIX]{x1D714}}_{D}(R)?\end{eqnarray}$$

$D$

Steady two-dimensional fluid flow over an obstacle is solved using complex variable methods. We consider the cases of rectangular obstacles, such as large boulders, submerged in a potential flow. These may arise in geophysics, marine and civil engineering. Our models are applicable to initiation of motion that may result in subsequent transport. The local flow depends on the obstacle shape, slowing down in confining corners and speeding up in expanding corners. The flow generates hydrodynamic forces, drag and lift, and their associated moments, which differ around each face. Our model replaces the need for ill-defined drag and lift coefficients with geometry-dependent functions. We predict smaller flow velocities to initiate motion. We show how a joint-bound boulder can be transported against gravity, and analyse the influence of a wake region behind an isolated boulder.

The second eigenvalue of the Robin Laplacian is shown to be maximal for the disk among simply-connected planar domains of fixed area when the Robin parameter is scaled by perimeter in the form $\unicode[STIX]{x1D6FC}/L(\unicode[STIX]{x1D6FA})$, and $\unicode[STIX]{x1D6FC}$ lies between $-2\unicode[STIX]{x1D70B}$ and $2\unicode[STIX]{x1D70B}$. Corollaries include Szegő’s sharp upper bound on the second eigenvalue of the Neumann Laplacian under area normalization, and Weinstock’s inequality for the first nonzero Steklov eigenvalue for simply-connected domains of given perimeter.

The first Robin eigenvalue is maximal, under the same conditions, for the degenerate rectangle. When area normalization on the domain is changed to conformal mapping normalization and the Robin parameter is positive, the maximiser of the first eigenvalue changes back to the disk.

At the ANZIAM conference in Hobart in February 2018, there were several talks on the solution of Laplace problems in multiply connected domains by means of conformal mapping. It appears to be not widely known that such problems can also be solved by the elementary method of series expansions with coefficients determined by least-squares fitting on the boundary. (These are not convergent series; the coefficients depend on the degree of the approximation.) Here we give a tutorial introduction to this method, which converges at an exponential rate if the boundary data are sufficiently well-behaved. The mathematical foundations go back to Runge in 1885 and Walsh in 1929. One of our examples involves an approximate Cantor set with up to 2048 components.

A problem from the class of unsteady plane flows of an ideal fluid with a free boundary is considered. A conformal mapping of the exterior of a unit circle onto the region occupied by the fluid is sought. The solution is constructed in the form of power series in time or Laurent series which are analytically continued with the use of Padé approximants and change of variables of a certain special type. The free boundary shape and the pressure and velocity distributions are found. Singularities of the solution are studied.

We prove that if Ω is a simply connected quadrature domain (QD) of a distribution with compact support and the point of infinity belongs to the boundary, then the boundary has an asymptotic curve that is a straight line, parabola or infinite ray. In other words, such QDs in the plane are perturbations of null QDs.

A problem of plane inertial motion of an ideal incompressible fluid with a free boundary, which initially has a quadratic velocity field, is studied by semi-analytical methods. A conformal mapping of the domain occupied by the fluid onto a unit circle is sought in the form of a power series with respect to time. Summation of series is performed by using Padé approximants.

This paper addresses a free boundary problem for a steady, uniform patch of vorticity surrounding a single flat plate of zero thickness and finite length. Exact solutions to this problem have previously been found in terms of conformal maps represented by Cauchy-type integrals. Here, however, it is demonstrated how, by considering an associated circular-arc polygon and using ideas from automorphic function theory, these maps can be expressed in a simple non-integral form.

Anti-plane interaction of an elliptically cylindrical layered media with an arbitrarily oriented crack embedded in an infinite matrix, intermediate layer, or inner inclusion under a remote uniform shear load is considered in this paper. Based on the technique of conformal mapping and the method of analytical continuation in conjunction with the alternating technique, the solution for a screw dislocation in the inclusions and the matrix is first derived in a series form. The integral equations with logarithmic singular kernels for a line crack can easily be obtained by using the screw dislocation solutions as the Green's function together with the principle superposition. The stress intensity factors, which can properly reflect the interaction between a crack and an elliptically cylindrical layered media, are then obtained numerically in terms of the values of the dislocation density functions of the integral equations. The effects of material property combinations and geometric parameters on the normalized mode-III stress intensity factors are discussed in detail and shown in graphic form.

In this paper, we review a number of uses of conformal mapping techniques for obtaining director profiles of liquid crystals in confined and semi-confined geometries. In particular, we will consider geometries which allow more than one stable state, some of which are of use in bistable displays. These solutions also allow the investigation of the energy of stable states and enable conclusions to be reached as to how such geometries may be optimised for bistable display applications. Such techniques are also able to provide initial configurations for the solution of more complicated situations where numerical methods are used to investigate switching characteristics.

Consider N towers each made up of a number of counters. At each step a tower is chosen at random, a counter removed which is then added to another tower also chosen at random. The probability distribution for the time needed to empty one of the towers is obtained in the case N = 3. Arguments are set forward as to why no simple formulae can be expected for N > 3. An asymptotic expression for the mean time before one of the towers becomes empty is derived in the case of four towers when they all initially contain a comparably large number of counters. We then study related problems, in particular the ruin problem for three players. Here we use simple martingale methodology as well as a solution proposed by T. S. Ferguson for a slightly modified problem. Throughout the paper it is our main objective to shed light on the reasons why the case N > 3 is so substantially different from the case N ≤ 3.

A technique is developed for the analysis of the asymptotic behaviour in the long run of queueing systems with two waiting lines. The generating function of the time-dependent joint queue-length distribution is obtained with the aid of the theory of boundary value problems of the Riemann–Hilbert type and by introducing a conformal mapping of the unit disk onto a given domain. In the asymptotic analysis an extensive use is made of theorems on the boundary behaviour of such conformal mappings.