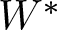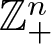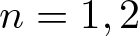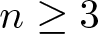1 results
Isometric dilations for representations of product systems
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 28 November 2024, pp. 1-42
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
-
We discuss representations of product systems (of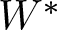
$W^*$-correspondences) over the semigroup 
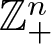$\mathbb{Z}^n_+$ and show that, under certain pureness and Szegö positivity conditions, a completely contractive representation can be dilated to an isometric representation. For 
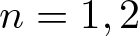$n=1,2$ this is known to hold in general (without assuming the conditions), but for 
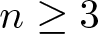$n\geq 3$, it does not hold in general (as is known for the special case of isometric dilations of a tuple of commuting contractions). Restricting to the case of tuples of commuting contractions, our result reduces to a result of Barik, Das, Haria, and Sarkar (Isometric dilations and von Neumann inequality for a class of tuples in the polydisc. Trans. Amer. Math. Soc. 372 (2019), 1429–1450). Our dilation is explicitly constructed, and we present some applications.
