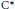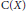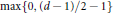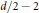1 results
On the Radius of Comparison of a Commutative C*-algebra
-
- Journal:
- Canadian Mathematical Bulletin / Volume 56 / Issue 4 / 01 December 2013
- Published online by Cambridge University Press:
- 20 November 2018, pp. 737-744
- Print publication:
- 01 December 2013
-
- Article
-
- You have access
- Export citation
-
Let
$X$ be a compact metric space. A lower bound for the radius of comparison of the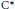 
${{\text{C}}^{*}}$-algebra 
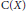$\text{C}\left( X \right)$ is given in terms of 
${{\dim}_{\mathbb{Q}}}\,X$, where ${{\dim}_{\mathbb{Q}}}\,X$ is the cohomological dimension with rational coefficients. If 
${{\dim}_{\mathbb{Q}}}\,X\,=\,\dim\,X\,=\,d$, then the radius of comparison of the 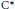${{\text{C}}^{*}}$-algebra 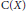$C\left( X \right)$ is 
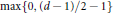$\max \left\{ 0,\,\left( d\,-\,1 \right)/\,2\,-\,1 \right\}$ if 
$d$ is odd, and must be either 
${d}/{2}\;\,-\,1$ or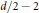 
${d}/{2}\;\,-\,2$ if $d$ is even (the possibility ${d}/{2}\;\,-\,1$ does occur, but we do not know if the possibility 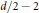${d}/{2}\;\,-\,2$ can also occur).
