We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
Let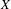 
$X$ be a finite-dimensional connected compact abelian group equipped with the normalized Haar measure 
$\unicode[STIX]{x1D707}$. We obtain the following mean ergodic theorem over ‘thin’ phase sets. Fix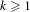 
$k\geq 1$ and, for every 
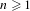$n\geq 1$, let 
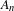$A_{n}$ be a subset of 
$\mathbb{Z}^{k}\cap [-n,n]^{k}$. Assume that 
$(A_{n})_{n\geq 1}$ has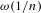 
$\unicode[STIX]{x1D714}(1/n)$ density in the sense that 
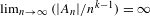$\lim _{n\rightarrow \infty }(|A_{n}|/n^{k-1})=\infty$. Let 
$T_{1},\ldots ,T_{k}$ be ergodic automorphisms of 
$X$. We have for any 
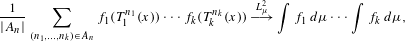$$\begin{eqnarray}\frac{1}{|A_{n}|}\mathop{\sum }_{(n_{1},\ldots ,n_{k})\in A_{n}}f_{1}(T_{1}^{n_{1}}(x))\cdots f_{k}(T_{k}^{n_{k}}(x))\stackrel{L_{\unicode[STIX]{x1D707}}^{2}}{\longrightarrow }\int f_{1}\,d\unicode[STIX]{x1D707}\cdots \int f_{k}\,d\unicode[STIX]{x1D707},\end{eqnarray}$$
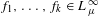$f_{1},\ldots ,f_{k}\in L_{\unicode[STIX]{x1D707}}^{\infty }$. When the 
$T_{i}$ are ergodic epimorphisms, the same conclusion holds under the further assumption that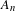 
$A_{n}$ is a subset of 
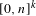$[0,n]^{k}$ for every 
$n$. The density assumption on the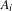 
$A_{i}$ is necessary. Immediate applications include certain Poincaré style recurrence results.
