We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
Let 
$\mathcal{V}$ be a variety of associative algebras generated by an algebra with 1 over a field of characteristic zero. This paper is devoted to the classification of the varieties $\mathcal{V}$ that are minimal of polynomial growth (i.e., their sequence of codimensions grows like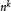 
${{n}^{k}}$, but any proper subvariety grows like 
${{n}^{t}}$ with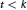 
$t\,<\,k$). These varieties are the building blocks of general varieties of polynomial growth.
It turns out that for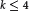 
$k\,\le \,4$ there are only a finite number of varieties of polynomial growth 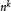${{n}^{k}}$, but for each 
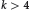$k\,>\,4$, the number of minimal varieties is at least 
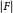$\left| F \right|$, the cardinality of the base field, and we give a recipe for their construction.
