We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We study cluster categories arising from marked surfaces (with punctures and non-empty boundaries). By constructing skewed-gentle algebras, we show that there is a bijection between tagged curves and string objects. Applications include interpreting dimensions of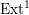 
$\operatorname{Ext}^{1}$ as intersection numbers of tagged curves and Auslander–Reiten translation as tagged rotation. An important consequence is that the cluster(-tilting) exchange graphs of such cluster categories are connected.
