We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We consider two sequences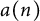 
$a(n)$ and 
$b(n)$,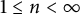 
$1\leq n<\infty $, generated by Dirichlet series 
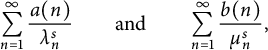$$ \begin{align*}\sum_{n=1}^{\infty}\frac{a(n)}{\lambda_n^{s}}\qquad\text{and}\qquad \sum_{n=1}^{\infty}\frac{b(n)}{\mu_n^{s}},\end{align*} $$
satisfying a familiar functional equation involving the gamma function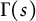 
$\Gamma (s)$. Two general identities are established. The first involves the modified Bessel function 
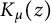$K_{\mu }(z)$, and can be thought of as a ‘modular’ or ‘theta’ relation wherein modified Bessel functions, instead of exponential functions, appear. Appearing in the second identity are 
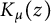$K_{\mu }(z)$, the Bessel functions of imaginary argument 
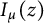$I_{\mu }(z)$, and ordinary hypergeometric functions 
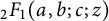${_2F_1}(a,b;c;z)$. Although certain special cases appear in the literature, the general identities are new. The arithmetical functions appearing in the identities include Ramanujan’s arithmetical function 
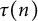$\tau (n)$, the number of representations of n as a sum of k squares 
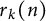$r_k(n)$, and primitive Dirichlet characters 
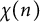$\chi (n)$.
