We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
$t_n$ CLASS INVARIANTS
We study the discriminants of the minimal polynomials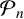 
$\mathcal {P}_n$ of the Ramanujan 
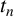$t_n$ class invariants, which are defined for positive 
$n\equiv 11\pmod {24}$. We show that 
$\Delta (\mathcal {P}_n)$ divides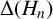 
$\Delta (H_n)$, where 
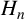$H_n$ is the ring class polynomial, with quotient a perfect square and determine the sign of 
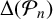$\Delta (\mathcal {P}_n)$ based on the ideal class group structure of the order of discriminant 
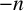$-n$. We also show that the discriminant of the number field generated by 
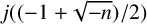$j({(-1+\sqrt {-n})}/{2})$, where j is the j-invariant, divides 
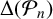$\Delta (\mathcal {P}_n)$. Moreover, using Ye’s computation of 
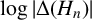$\log|\Delta(H_n)|$ [‘Revisiting the Gross–Zagier discriminant formula’, Math. Nachr. 293 (2020), 1801–1826], we show that 3 never divides 
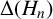$\Delta(H_n)$, and thus 
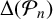$\Delta(\mathcal{P}_n)$, for all squarefree 
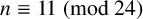$n\equiv11\pmod{24}$.
