In this paper, we characterize amenability of locally compact groups in terms of the properties of Orlicz Figà-Talamanca Herz algebras.

For a locally compact group $G$, let 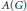$A(G)$ be its Fourier algebra, let ${{M}_{cb}}A(G)$ denote the completely bounded multipliers of 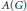$A(G)$, and let ${{A}_{Mcb}}\,(G)$ stand for the closure of 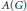$A(G)$ in ${{M}_{cb}}A(G)$. We characterize the norm one idempotents in ${{M}_{cb}}A(G)$: the indicator function of a set 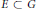$E\,\subset \,G$ is a norm one idempotent in ${{M}_{cb}}A(G)$ if and only if $E$ is a coset of an open subgroup of $G$. As applications, we describe the closed ideals of ${{A}_{Mcb}}\,(G)$ with an approximate identity bounded by 1, and we characterize those $G$ for which ${{A}_{Mcb}}\,(G)$ is 1-amenable in the sense of B. E. Johnson. (We can even slightly relax the norm bounds.)

Let $G$ be a $\sigma$-compact, locally compact group and $\mathcal I$ be a closed 2-sided ideal with finite codimension in $L^1(G)$. It is shown that there are a closed left ideal ${\mathcal L}$ having a right bounded approximate identity and a closed right ideal ${\mathcal R}$ having a left bounded approximate identity such that ${\mathcal I} = {\mathcal L} + {\mathcal R}$. The proof uses ideas from the theory of boundaries of random walks on groups. 2000 Mathematics Subject Classification: primary 43A20; secondary 42A85, 43A07, 46H10, 46H40, 60B11.

Closed ideals in A(G) with bounded approximate identities are characterized for amenable [SIN]-groups and arbitrary discrete groups. This extends a result of Liu, van Rooij and Wang for abelian groups.