Let  $G$ be a locally compact group and let
$G$ be a locally compact group and let  $\omega$ be a continuous weight on
$\omega$ be a continuous weight on  $G$. We show that for each of the Banach algebras
$G$. We show that for each of the Banach algebras  ${{L}^{1}}\left( G,\,\omega \right),\,M\left( G,\,\omega \right),\,LUC{{\left( G,\,{{\omega }^{-1}} \right)}^{*}}$, and
${{L}^{1}}\left( G,\,\omega \right),\,M\left( G,\,\omega \right),\,LUC{{\left( G,\,{{\omega }^{-1}} \right)}^{*}}$, and 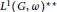 ${{L}^{1}}{{\left( G,\,\omega \right)}^{**}}$, the order structure combined with the algebra structure determines the weighted group.
${{L}^{1}}{{\left( G,\,\omega \right)}^{**}}$, the order structure combined with the algebra structure determines the weighted group.