We consider two questions on the geometry of Lipschitz-free $p$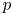-spaces $\mathcal {F}_p$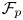, where $0< p\leq 1$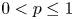, over subsets of finite-dimensional vector spaces. We solve an open problem and show that if $(\mathcal {M}, \rho )$ 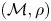is an infinite doubling metric space (e.g. an infinite subset of an Euclidean space), then $\mathcal {F}_p (\mathcal {M}, \rho ^\alpha )\simeq \ell _p$ 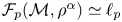for every $\alpha \in (0,\,1)$ 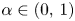and $0< p\leq 1$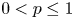. An upper bound on the Banach–Mazur distance between the spaces $\mathcal {F}_p ([0, 1]^d, |\cdot |^\alpha )$ 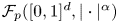and $\ell _p$ 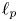is given. Moreover, we tackle a question due to Albiac et al. 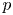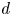[4] and expound the role of $p$, $d$ for the Lipschitz constant of a canonical, locally coordinatewise affine retraction from $(K, |\cdot |_1)$, where $K=\cup _{Q\in \mathcal {R}} Q$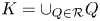 is a union of a collection $\emptyset \neq \mathcal {R} \subseteq \{ Rw + R[0,\,1]^d: w\in \mathbb {Z}^d\}$ 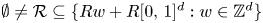of cubes in $\mathbb {R}^d$ 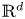with side length $R>0$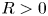, into the Lipschitz-free $p$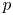-space $\mathcal {F}_p (V, |\cdot |_1)$ 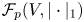over their vertices.

We prove a general principle satisfied by weakly precompact sets of Lipschitz-free spaces. By this principle, certain infinite dimensional phenomena in Lipschitz-free spaces over general metric spaces may be reduced to the same phenomena in free spaces over their compact subsets. As easy consequences we derive several new and some known results. The main new results are: $\mathcal {F}(X)$ is weakly sequentially complete for every superreflexive Banach space $X$, and $\mathcal {F}(M)$ has the Schur property and the approximation property for every scattered complete metric space $M$.

We prove that a wide class of strongly proper forcing posets have quotients with strong properties. Specifically, we prove that quotients of forcing posets which have universal strongly generic conditions on a stationary set of models by certain nice regular suborders satisfy the ω1-approximation property. We prove that the existence of stationarily many ω1-guessing models in Pω2(H(θ)), for sufficiently large cardinals θ, is consistent with the continuum being arbitrarily large, solving a problem of Viale and Weiss [13].

New necessary and sufficient conditions are established for Banach spaces to have the approximation property; these conditions are easier to check than the known ones. A shorter proof of a result of Grothendieck is presented, and some properties of a weak version of the approximation property are addressed.

Let $X$ be a Banach space and let $Y$ be a closed subspace of a Banach space $Z$. The following theorem is proved. Assume that $X^*$ or $Z^*$ has the approximation property. If there exists a bounded linear extension operator from $Y^*$ to $Z^*$, then any bounded linear operator $T:X\rightarrow Y$ is nuclear whenever $T$ is nuclear from $X$ to $Z$. The particular case of the theorem with $Z=Y^{**}$ is due to Grothendieck and Oja and Reinov. Numerous applications are presented. For instance, it is shown that a bounded linear operator $T$ from an arbitrary Banach space $X$ to an $\mathcal{L}_\infty$-space $Y$ is nuclear whenever $T$ is nuclear from $X$ to some Banach space $Z$ containing $Y$ as a subspace.

AMS 2000 Mathematics subject classification: Primary 46B20; 46B28; 47B10

We give an example of a Banach space X such that K (X, X) is not an ideal in K (X, X**). We prove that if z* is a weak* denting point in the unit ball of Z* and if X is a closed subspace of a Banach space Y, then the set of norm-preserving extensions H B(x* ⊗ z*) ⊆ (Z*, Y)* of a functional x* ⊗ Z* ∈ (Z ⊗ X)* is equal to the set H B(x*) ⊗ {z*}. Using this result, we show that if X is an M-ideal in Y and Z is a reflexive Banach space, then K (Z, X) is an M-ideal in K(Z, Y) whenever K (Z, X) is an ideal in K (Z, Y). We also show that K (Z, X) is an ideal (respectively, an M-ideal) in K (Z, Y) for all Banach spaces Z whenever X is an ideal (respectively, an M-ideal) in Y and X * has the compact approximation property with conjugate operators.