We establish that the existence of a winning strategy in certain topological games, closely related to a strong game of Choquet, played in a topological space 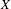$X$ and its hyperspace 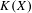$K(X)$ of all nonempty compact subsets of 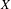$X$ equipped with the Vietoris topology, is equivalent for one of the players. For a separable metrizable space 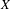$X$, we identify a game-theoretic condition equivalent to $K(X)$ being hereditarily Baire. It implies quite easily a recent result of Gartside, Medini and Zdomskyy that characterizes hereditary Baire property of hyperspaces $K(X)$ over separable metrizable spaces $X$ via the Menger property of the remainder of a compactification of 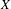$X$. Subsequently, we use topological games to study hereditary Baire property in spaces of probability measures and in hyperspaces over filters on natural numbers. To this end, we introduce a notion of strong $P$-filter ${\mathcal{F}}$ and prove that it is equivalent to 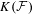$K({\mathcal{F}})$ being hereditarily Baire. We also show that if 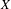$X$ is separable metrizable and 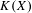$K(X)$ is hereditarily Baire, then the space $P_{r}(X)$ of Borel probability Radon measures on 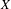$X$ is hereditarily Baire too. It follows that there exists (in ZFC) a separable metrizable space 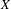$X$, which is not completely metrizable with 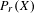$P_{r}(X)$ hereditarily Baire. As far as we know, this is the first example of this kind.

In this paper, I will give a new characterisation of the spaces of complete theories of pseudofinite fields and of algebraically closed fields with a generic automorphism (ACFA) in terms of the Vietoris topology on absolute Galois groups of prime fields.

Let LSC(X) denote the set of extended real valued lower semicontinuous functions on a metrizable space X. If f, f1, f2, f3,... is a sequence in LSC(X), we say 〈fn〉 is epi-convergent to f provided the sequence of epigraphs 〈epi fn〉 is Kuratowski- Painlevé convergent to epi f. In this note we address the following question: what conditions on f and/or on X are necessary and sufficient for this mode of convergence to force epigraphical convergence with respect to the stronger Hausdorff metric and Vietoris topologies?