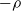We consider a one-dimensional superprocess with a supercritical local branching mechanism $\psi$, where particles move as a Brownian motion with drift $-\rho$ and are killed when they reach the origin. It is known that the process survives with positive probability if and only if 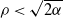$\rho<\sqrt{2\alpha}$, where $\alpha=-\psi'(0)$. When $\rho<\sqrt{2 \alpha}$, Kyprianou et al. [18] proved that 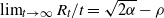$\lim_{t\to \infty}R_t/t =\sqrt{2\alpha}-\rho$ almost surely on the survival set, where $R_t$ is the rightmost position of the support at time t. Motivated by this work, we investigate its large deviation, in other words, the convergence rate of $\mathbb{P}_{\delta_x} (R_t >\gamma t+\theta)$ as $t \to \infty$, where $\gamma >\sqrt{2 \alpha} -\rho$, 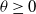$\theta \ge 0$. As a by-product, a related Yaglom-type conditional limit theorem is obtained. Analogous results for branching Brownian motion can be found in Harris et al. [13].

We establish the moderate deviation principle for the solutions of a class of stochastic partial differential equations with non-Lipschitz continuous coefficients. As an application, we derive the moderate deviation principle for two important population models: super-Brownian motion and the Fleming–Viot process.

In this paper we establish the central limit theorem for a class of stochastic partial differential equations and as an application derive this theorem for two widely studied population models: super-Brownian motion and the Fleming-Viot process.

We analyse the behaviour of supercritical super-Brownian motion with a barrier through the pathwise backbone embedding of Berestycki, Kyprianou and Murillo-Salas (2011). In particular, by considering existing results for branching Brownian motion due to Harris and Kyprianou (2006) and Maillard (2011), we obtain, with relative ease, conclusions regarding the growth in the right-most point in the support, analytical properties of the associated one-sided Fisher-Kolmogorov-Petrovskii-Piscounov wave equation, as well as the distribution of mass on the exit measure associated with the barrier.

In this article we investigate a class of superprocess with cut-off branching, studying the long-time behavior of the occupation time process. Persistence of the process holds in all dimensions. Central-limit-type theorems are obtained, and the scales are dimension dependent. The Gaussian limit holds only when d ≤ 4. In dimension one, a full large deviation principle is established and the rate function is identified explicitly. Our result shows that the super-Brownian motion with cut-off branching in dimension one has many features that are similar to super-Brownian motion in dimension three.

We derive a large-deviation principle for super-Brownian motion with immigration, where the immigration is governed by the Lebesgue measure. We show that the speed function is t 1/2 for d = 1, t/logt for d = 2 and t for d ≥ 3, which is different from that of the occupation-time process counterpart (without immigration) and the model of random immigration.

We prove some central limit theorems for a two-level super-Brownian motion with random immigration, which lead to limiting Gaussian random fields. The covariances of those Gaussian fields are explicitly characterized.

Moderate deviation principles are established in dimensions d ≥ 3 for super-Brownian motion with random immigration, where the immigration rate is governed by the trajectory of another super-Brownian motion. It fills in the gap between the central limit theorem and large deviation principles for this model which were obtained by Hong and Li (1999) and Hong (2001).

We prove a central limit theorem for the super-Brownian motion with immigration governed by another super-Brownian. The limit theorem leads to Gaussian random fields in dimensions d ≥ 3. For d = 3 the field is spatially uniform; for d ≥ 5 its covariance is given by the potential operator of the underlying Brownian motion; and for d = 4 it involves a mixture of the two kinds of fluctuations.

Let X be a d-dimensional continuous super-Brownian motion with branching rate ε, which might be described symbolically by the "stochastic equation" a space-time white noise. A Schilder type theorem is established concerning large deviation probabilities of X on path space as ε → 0, with a representation of the rate functional via an L2 -functional on a generalized "Cameron-Martin space" of measure-valued paths.