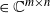We explore the limiting spectral distribution of large-dimensional random permutation matrices, assuming the underlying population distribution possesses a general dependence structure. Let $\textbf X = (\textbf x_1,\ldots,\textbf x_n)$ $\in \mathbb{C} ^{m \times n}$ be an $m \times n$ data matrix after self-normalization (n samples and m features), where $\textbf x_j = (x_{1j}^{*},\ldots, x_{mj}^{*} )^{*}$. Specifically, we generate a permutation matrix $\textbf X_\pi$ by permuting the entries of $\textbf x_j$ $(j=1,\ldots,n)$ and demonstrate that the empirical spectral distribution of $\textbf {B}_n = ({m}/{n})\textbf{U} _{n} \textbf{X} _\pi \textbf{X} _\pi^{*} \textbf{U} _{n}^{*}$ weakly converges to the generalized Marčenko–Pastur distribution with probability 1, where $\textbf{U} _n$ is a sequence of 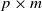$p \times m$ non-random complex matrices. The conditions we require are $p/n \to c >0$ and $m/n \to \gamma > 0$.

This paper provides tools for the study of the Dirichlet random walk in Rd. We compute explicitly, for a number of cases, the distribution of the random variable W using a form of Stieltjes transform of W instead of the Laplace transform, replacing the Bessel functions with hypergeometric functions. This enables us to simplify some existing results, in particular, some of the proofs by Le Caër (2010), (2011). We extend our results to the study of the limits of the Dirichlet random walk when the number of added terms goes to ∞, interpreting the results in terms of an integral by a Dirichlet process. We introduce the ideas of Dirichlet semigroups and Dirichlet infinite divisibility and characterize these infinite divisible distributions in the sense of Dirichlet when they are concentrated on the unit sphere of Rd.

Some properties of the generalized Goodwin–Staton integral are derived. Explicit error bounds for the asymptotic expansion are determined. In addition, results are obtained for the oscillatory case and when logarithmic factors are present.

In the random walk whose state space is a subset of the non-negative integers explicit representations for the generating functions of the n-step transition and the first return probabilities are obtained. These representations involve the Stieltjes transform of the spectral measure of the process and the corresponding orthogonal polynomials. Several examples are given in order to illustrate the application of the results.