We exhibit the first explicit examples of Salem sets in ℚp of every dimension 0 < α < 1 by showing that certain sets of well-approximable p-adic numbers are Salem sets. We construct measures supported on these sets that satisfy essentially optimal Fourier decay and upper regularity conditions, and we observe that these conditions imply that the measures satisfy strong Fourier restriction inequalities. We also partially generalize our results to higher dimensions. Our results extend theorems of Kaufman, Papadimitropoulos, and Hambrook from the real to the p-adic setting.

We study the regularity of convolution powers for measures supported on Salem sets, and prove related results on Fourier restriction and Fourier multipliers. In particular we show that for $\alpha $ of the form $d\,/\,n,\,n\,=\,2,3,...$ there exist $\alpha $-Salem measures for which the ${{L}^{2}}$ Fourier restriction theorem holds in the range 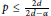$p\,\le \,\frac{2d}{2d\,-\,\alpha }$. The results rely on ideas of Körner. We extend some of his constructions to obtain upper regular $\alpha $-Salem measures, with sharp regularity results for $n$-fold convolutions for all $n\,\in \,\mathbb{N}$.