Outdoor air pollution is estimated to cause a huge number of premature deaths worldwide. It catalyzes many diseases on a variety of time scales, and it has a detrimental effect on the environment. In light of these impacts, it is necessary to obtain a better understanding of the dynamics and statistics of measured air pollution concentrations, including temporal fluctuations of observed concentrations and spatial heterogeneities. Here, we present an extensive analysis for measured data from Europe. The observed probability density functions (PDFs) of air pollution concentrations depend very much on the spatial location and the pollutant substance. We analyze a large number of time series data from 3544 different European monitoring sites and show that the PDFs of nitric oxide ($ NO $), nitrogen dioxide ($ {NO}_2 $), and particulate matter ($ {PM}_{10} $ and $ {PM}_{2.5} $) concentrations generically exhibit heavy tails. These are asymptotically well approximated by $ q $-exponential distributions with a given entropic index $ q $ and width parameter $ \lambda $. We observe that the power-law parameter $ q $ and the width parameter $ \lambda $ vary widely for the different spatial locations. We present the results of our data analysis in the form of a map that shows which parameters $ q $ and $ \lambda $ are most relevant in a given region. A variety of interesting spatial patterns is observed that correlate to the properties of the geographical region. We also present results on typical time scales associated with the dynamical behavior.

Growth-fragmentation processes describe the evolution of systems in which cells grow slowly and fragment suddenly. Despite originating as a way to describe biological phenomena, they have recently been found to describe the lengths of certain curves in statistical physics models. In this note, we describe a new growth-fragmentation process connected to random planar maps with faces of large degree, having as a key ingredient the ricocheted stable process recently discovered by Budd. The process has applications to the excursions of planar Brownian motion and Liouville quantum gravity.

Let 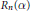${{R}_{n}}\left( \alpha \right)$ be the 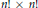$n!\,\times \,n!$ matrix whose matrix elements 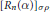${{\left[ {{R}_{n}}\left( \alpha \right) \right]}_{\sigma p}}$ , with $\sigma$ and $p$ in the symmetric group ${{G}_{n}}$ , are ${{\alpha }^{\ell \left( \sigma {{p}^{-1}} \right)}}$ with 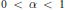$0\,<\,\alpha \,<\,1$, where 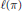$\ell \left( \text{ }\!\!\pi\!\!\text{ } \right)$ denotes the number of cycles in 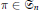$\text{ }\pi \text{ }\in {{G}_{n}}.$ We give the spectrum of 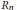${{R}_{n}}$ and show that the ratio of the largest eigenvalue 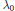${{\text{ }\!\!\lambda\!\!\text{ }}_{0}}$ to the second largest one (in absolute value) increases as a positive power of $n$ as 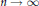$n\,\to \,\infty$.

The fluctuation of the counts of particles in m regions are used to yield an estimate of a fundamental motion parameter. The effect of varying m on the precision of the estimation method is considered. An exact analysis and simulation of the Fürth pedestrian vector process is presented.

This article deals with the generalized Smoluchowski process, {n(t), t ≧ 0}, defined by the temporal fluctuating of the numbers of randomly moving particles contained in m < ∞ disjoint regions of space. The relationship of the Smoluchowski process {n(t), t ≧ 0} to the emigration–immigration process is discussed and conditions for their equivalence are presented.