Let I(x, u) be the probability that two genes found a vector distance x apart are the same type in an infinite-allele selectively-neutral migration model with mutation rate u. The creatures involved inhabit an infinite of colonies, are diploid and are held at N per colony. Set  in one dimension and
in one dimension and 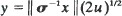 in higher dimensions, where σ2 is the covariance matrix of the migration law (which is assumed to have finite fifth moments). Then
in higher dimensions, where σ2 is the covariance matrix of the migration law (which is assumed to have finite fifth moments). Then 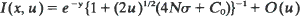 in one dimension,
in one dimension, 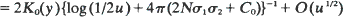 in two dimensions, and
in two dimensions, and 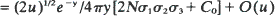 in three dimensions uniformly for
in three dimensions uniformly for 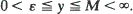 Here C0 is a constant depending on the migration law, K0(y) is the Bessel function of the second kind of order zero, and
Here C0 is a constant depending on the migration law, K0(y) is the Bessel function of the second kind of order zero, and  are the eigenvalues of σ2. For symmetric nearest-neighbor migrations,
are the eigenvalues of σ2. For symmetric nearest-neighbor migrations, 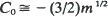 in one dimension and
in one dimension and 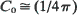 log mi in two. For
log mi in two. For  is known in one dimension and C0 does not appear. In two dimensions,
is known in one dimension and C0 does not appear. In two dimensions, 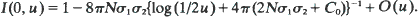 These results extend and make more precise earlier work of Malécot, Weiss and Kimura and Nagylaki.
These results extend and make more precise earlier work of Malécot, Weiss and Kimura and Nagylaki.

 in one dimension and
in one dimension and 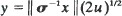 in higher dimensions, where σ
in higher dimensions, where σ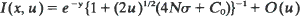 in one dimension,
in one dimension, 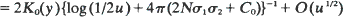 in two dimensions, and
in two dimensions, and 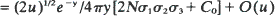 in three dimensions uniformly for
in three dimensions uniformly for 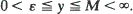 Here
Here  are the eigenvalues of σ
are the eigenvalues of σ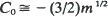 in one dimension and
in one dimension and 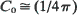 log
log  is known in one dimension and
is known in one dimension and 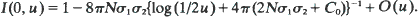 These results extend and make more precise earlier work of Malécot, Weiss and Kimura and Nagylaki.
These results extend and make more precise earlier work of Malécot, Weiss and Kimura and Nagylaki.