Let  $w$ be either in the Muckenhoupt class of
$w$ be either in the Muckenhoupt class of 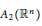 ${{A}_{2}}\left( {{\mathbb{R}}^{n}} \right)$ weights or in the class of
${{A}_{2}}\left( {{\mathbb{R}}^{n}} \right)$ weights or in the class of 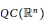 $QC\left( {{\mathbb{R}}^{n}} \right)$ weights, and let
$QC\left( {{\mathbb{R}}^{n}} \right)$ weights, and let 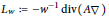 ${{L}_{w}}\,:=\,-{{w}^{-1}}\,\text{div}\left( A\nabla \right)$ be the degenerate elliptic operator on the Euclidean space
${{L}_{w}}\,:=\,-{{w}^{-1}}\,\text{div}\left( A\nabla \right)$ be the degenerate elliptic operator on the Euclidean space  ${{\mathbb{R}}^{n}}$,
${{\mathbb{R}}^{n}}$,  $n\,\ge \,2$. In this article, the authors establish the non-tangential maximal function characterization of the Hardy space
$n\,\ge \,2$. In this article, the authors establish the non-tangential maximal function characterization of the Hardy space 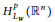 $H_{{{L}_{w}}}^{p}\,\left( {{\mathbb{R}}^{n}} \right)$ associated with
$H_{{{L}_{w}}}^{p}\,\left( {{\mathbb{R}}^{n}} \right)$ associated with 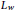 ${{L}_{w}}$ for
${{L}_{w}}$ for 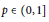 $p\,\in \,(0,\,1]$, and when
$p\,\in \,(0,\,1]$, and when 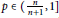 $p\,\in \,(\frac{n}{n+1},\,1]$ and
$p\,\in \,(\frac{n}{n+1},\,1]$ and  $w\,\in \,{{A}_{{{q}_{0}}}}\left( {{\mathbb{R}}^{n}} \right)$ with
$w\,\in \,{{A}_{{{q}_{0}}}}\left( {{\mathbb{R}}^{n}} \right)$ with  ${{q}_{0}}\,\in \,[1,\,\frac{p(n+1)}{n})$, the authors prove that the associated Riesz transform
${{q}_{0}}\,\in \,[1,\,\frac{p(n+1)}{n})$, the authors prove that the associated Riesz transform  $\nabla L_{w}^{-1/2}$ is bounded from
$\nabla L_{w}^{-1/2}$ is bounded from 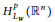 $H_{{{L}_{w}}}^{p}\,\left( {{\mathbb{R}}^{n}} \right)$ to the weighted classical Hardy space
$H_{{{L}_{w}}}^{p}\,\left( {{\mathbb{R}}^{n}} \right)$ to the weighted classical Hardy space 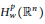 $H_{w}^{p}\left( {{\mathbb{R}}^{n}} \right)$.
$H_{w}^{p}\left( {{\mathbb{R}}^{n}} \right)$.
 $L^{q}$ ESTIMATES OF RIESZ TRANSFORMS ASSOCIATED TO SCHRÖDINGER OPERATORS
$L^{q}$ ESTIMATES OF RIESZ TRANSFORMS ASSOCIATED TO SCHRÖDINGER OPERATORS