The quaternion is a powerful and common tool to avoid singularity in rotational dynamics in three-dimensional (3D) space. Here it has been particularly used as an alternative to Euler angles and rotation matrix. The application of the quaternion is exercised in quadrotor modeling and control. It changes the dynamics and represents a singularity-free attitude model. Here for the first time (for the best knowledge of authors), the state-dependent differential Riccati equation (SDDRE) control has been implemented on the quaternion-based model of a quadcopter. The proposed control structure is capable of aerobatic flight, and the Pugachev’s Cobra maneuver is chosen to assess the capability of the quaternion-based SDDRE approach. The introduced control simulator is validated by comparison with conventional dynamics based on Euler angles, controlled using a proportional-derivative (PD) controller on a normal regulation flight. The simulator successfully performed the Cobra maneuver and also validated the proposed structure. The more precision in regulation along with lower energy consumption demonstrated the superiority of the introduced approach.

This paper introduces an intuitive and safe command approach for a quadrotor, where inertial and muscular gestures are used for semi-autonomous flight. A bracelet composed of gyroscopes, accelerometers, and electromyographic sensors is used to detect user gestures, then an algorithm is proposed to interpret the signals as flight commands. The main goal is to provide a wearable, easy-to-handle human–machine interface for users a to safely command this kind of vehicles, even for inexpert operators. Safety measures are incorporated in the scheme to further enhance the user’s experience. Experimental tests are performed to validate the proposal.

Heading errors caused by gyroscope drift affect the positioning precision of pedestrian dead reckoning, and these errors are even greater for smartphone-based reckoning. In this study, an optimised improved heuristic drift elimination (O-iHDE) method is proposed to correct the heading errors on a smartphone gyroscope. Based on an analysis of the improved heuristic drift elimination (iHDE) and enhanced improved heuristic drift elimination (E-iHDE) algorithms, the quaternion method is used to update the attitude and angle threshold judgement conditions, and a method for correcting the quaternion is added to eliminate the heading errors caused by random gyro errors. The analysis of multiple sets of experiments shows that the new method improves the ability to discern and correct the walking route, and the heading accuracy is improved by more than 90%, which extends the effective operation time of pedestrian dead reckoning positioning based on the step-by-step system.

The UnScented QUaternion Estimator (USQUE) has been approved as a promising substitute for the extended Kalman filter when applied in the Standard Inertial Navigation Equations (SINE)-based inertial navigation system/global positioning system integration. However, the expensive computational burden makes it untenable in real time applications. In this paper, a computationally efficient filtering algorithm called Marginalised USQUE (MUSQUE) is derived by embedding the Marginalised Unscented Transformation (MUT) that is applicable to nonlinear systems with a linear substructure into the widely used USQUE. The contributions of the MUSQUE developed here are twofold. Firstly, the SINE are reconstructed to be only nonlinear in the attitude quaternion while linear in velocity and position, which makes the MUT potentially applicable in the USQUE. Secondly, the quaternion and generalised Rodrigues parameter-based sigma points are propagated simultaneously in the MUSQUE to deal with the dimensional mismatching hierarchy of the USQUE. Compared with the USQUE the number of sigma points can be decreased substantially, thereby making the applied MUSQUE computationally tenable. The experimental results show that the proposed MUSQUE has nearly identical performance with the USQUE but with much reduced computational burden.

A novel relative spacecraft attitude and position estimation approach based on an Unscented Kalman Filter (UKF) is derived. The integrated sensor suite comprises the gyro sensors on each spacecraft and a vision-based navigation system on the slave spacecraft. In the traditional algorithm, an assumption that the master's body frame coincides with its Local Vertical Local Horizontal (LVLH) frame is made to construct the line-of-sight observations for convenience. To solve this problem, two relative quaternions that map the master's LVLH frame to the slave and master body frames are involved. The general relative equations of motion for eccentric orbits are used to describe the positional dynamics. The implementation equations for the UKF are derived. A modified version of the UKF is presented based on the averaging-quaternion algorithm. Simulation results indicate that the proposed filters provide more accurate estimates of relative attitude and position than the Extended Kalman Filter (EKF).

Positioning and navigation data for unmanned surface vehicles (USVs) are extracted using the Global Positioning System (GPS) and the Inertial Navigation System (INS) integrated with an inertial measurement unit (IMU). The integration of quaternion with direction cosine matrix (DCM) with the aim of obtaining high accuracy with complete system independence has been effectively used to supply position and attitude information for autonomous navigation of marine crafts. A DCM integrated with a quaternion provided an advanced technique for precise USV attitude estimation and position determination using low-cost sensors. This paper presents the implementation of an INS developed by the integration of DCM and quaternion.

In this paper, we investigate the controllability of an underwater vehicle immersed in an infinite volume of an inviscid fluid whose flow is assumed to be irrotational. Taking as control input the flow of the fluid through a part of the boundary of the rigid body, we obtain a finite-dimensional system similar to Kirchhoff laws in which the control input appears through both linear terms (with time derivative) and bilinear terms. Applying Coron’s return method, we establish some local controllability results for the position and velocities of the underwater vehicle. Examples with six, four, or only three controls inputs are given for a vehicle with an ellipsoidal shape.

A simple algorithm is developed and implemented to eliminate ambiguities, in both statistical analyses of orientation data (e.g., orientation averaging) and electron backscattered diffraction (EBSD) orientation map visualization, caused by symmetrically equivalent orientations and the wrap-around or umklapp effect. Using crystal symmetry operators and the lowest Euclidian-distance criterion, the orientation of each pixel within a grain is redefined. An advantage of this approach is demonstrated for direct determination of the representative orientation of a grain within an EBSD map by mean, median, or quaternion-based averaging methods that can be further used within analyses or visualization of misorientation or geometrically necessary dislocation (GND) density. If one also considers the lattice curvature tensor, five components of the dislocation density tensor—corresponding to a part of the GND content—may be inferred. The methodology developed is illustrated using EBSD orientation data obtained from the fatigue crack-tips/wakes in aerospace aluminum alloys 2024-T351 and 7050-T7451.

Let (M,I,J,K) be a compact hyperkähler manifold, 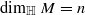, and L a non-trivial holomorphic line bundle on (M,I). Using the quaternionic Dolbeault complex, we prove the following vanishing theorem for holomorphic cohomology of L. If c1(L) lies in the closure of the dual Kähler cone, then Hi(L)=0 for i>n. If c1(L) lies in the opposite cone 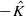, then Hi(L)=0 for i<n. Finally, if c1(L) is neither in nor in 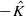, then Hi(L)=0 for .

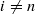Based on the identification of four-dimensional Möbius transformations

$$ g(x)=(ax+b)(cx+d)^{-1} $$

by the matrix group $\mathrm{PS}_\triangle L(2,\mathbb{H})$ of quaternionic $2\times2$ matrices with Dieudonné determinant equal to $1$, we give an explicit expression for the classification of $g$ in terms of $a$, $b$, $c$ and $d$.

Rotational data in the form of measured three-dimensional rotations or orientations arise naturally in many fields of science, including biomechanics, orthopaedics and robotics. The cyclic topology of rotation spaces calls for special care and considerations when performing statistical analysis of rotational data. Relevant theory has been developed during the last three decades, and has become a standard tool in some areas. In relation to the study of human kinematics and motion however, these concepts have hardly been put to use. This paper gives an introduction to the intricacies of three-dimensional rotations, and provides a thorough geometric interpretation of several approaches to averaging rotational data. A set of novel, simple operators is presented. Simulations and a prosthetics-related real-world example involving wrist kinematics illuminate important aspects of the results. Finally generalizations and related subjects for further research are suggested.