We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
In this paper, we are concerned with the physically engaging pseudo-relativistic Schrödinger system:
\[ \begin{cases} \left(-\Delta+m^{2}\right)^{s}u(x)=f(x,u,v,\nabla u) & \hbox{in } \Omega,\\ \left(-\Delta+m^{2}\right)^{t}v(x)=g(x,u,v,\nabla v) & \hbox{in } \Omega,\\ u>0,v>0 & \hbox{in } \Omega, \\ u=v\equiv 0 & \hbox{in } \mathbb{R}^{N}\setminus\Omega, \end{cases} \]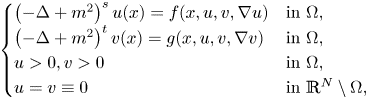where $s,t\in (0,1)$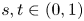
and the mass $m>0.$
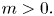By using the direct method of moving plane, we prove the strict monotonicity, symmetry and uniqueness for positive solutions to the above system in a bounded domain, unbounded domain, $\mathbb {R}^{N}$
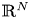, $\mathbb {R}^{N}_{+}$
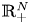and a coercive epigraph domain $\Omega$
in $\mathbb {R}^{N}$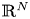
, respectively.
