We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
Let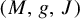 
$(M,g,J)$ be a closed Kähler manifold with negative sectional curvature and complex dimension 
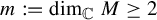$m := \dim _{\mathbb {C}} M \geq 2$. In this article, we study the unitary frame flow, that is, the restriction of the frame flow to the principal 
$\mathrm {U}(m)$-bundle 
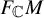$F_{\mathbb {C}}M$ of unitary frames. We show that if 
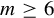$m \geq 6$ is even and 
$m \neq 28$, there exists 
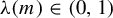$\unicode{x3bb} (m) \in (0, 1)$ such that if 
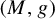$(M, g)$ has negative 
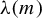$\unicode{x3bb} (m)$-pinched holomorphic sectional curvature, then the unitary frame flow is ergodic and mixing. The constants 
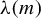$\unicode{x3bb} (m)$ satisfy 
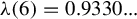$\unicode{x3bb} (6) = 0.9330...$, 
$\lim _{m \to +\infty } \unicode{x3bb} (m) = {11}/{12} = 0.9166...$, and 
$m \mapsto \unicode{x3bb} (m)$ is decreasing. This extends to the even-dimensional case the results of Brin and Gromov [On the ergodicity of frame flows. Invent. Math. 60(1) (1980), 1–7] who proved ergodicity of the unitary frame flow on negatively curved compact Kähler manifolds of odd complex dimension.
