We consider d-dimensional stochastic processes 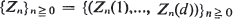 which take values in (R+)d These processes generalize Galton-Watson branching processes, but the main assumption of branching processes, independence between particles, is dropped. Instead, we assume for some
which take values in (R+)d These processes generalize Galton-Watson branching processes, but the main assumption of branching processes, independence between particles, is dropped. Instead, we assume for some 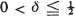
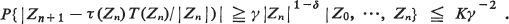
Here τ:(R+)d→R +, |x| = σ1d |x(i)|, A {x ∈(R+)d: |x| 1} and T: A→A. Under various assumptions on the maps τ and T it is shown that with probability one there exists a ρ > 1, a fixed point p ∈ A of T and a random variable w such that limn→∞Zn|ρnwp. This result is a generalization of the main limit theorem for supercritical branching processes; note, however, that in the present situation both ρ and ρ are random as well. The results are applied to a population genetical model for zygotic selection without mutation at one locus.