Let $L=-\Delta +V$ be a Schrödinger operator in ${\mathbb R}^n$ with $n\geq 3$, where $\Delta $ is the Laplace operator denoted by $\Delta =\sum ^{n}_{i=1}({\partial ^{2}}/{\partial x_{i}^{2}})$ and the nonnegative potential V belongs to the reverse Hölder class $(RH)_{q}$ with $q>n/2$. For $\alpha \in (0,1)$, we define the operator

$$ \begin{align*} T_N^{L^{\alpha}} f(x) =\sum_{j=N_1}^{N_2} v_j(e^{-a_{j+1}L^\alpha} f(x)-e^{-a_{j}L^\alpha} f(x)) \quad \mbox{for all }x\in \mathbb R^n, \end{align*} $$

where 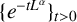$\{e^{-tL^\alpha } \}_{t>0}$ is the fractional heat semigroup of the operator L, 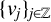$\{v_j\}_{j\in \mathbb Z}$ is a bounded real sequence and $\{a_j\}_{j\in \mathbb Z}$ is an increasing real sequence.

We investigate the boundedness of the operator $T_N^{L^{\alpha }}$ and the related maximal operator $T^*_{L^{\alpha }}f(x):=\sup _N \vert T_N^{L^{\alpha }} f(x)\vert $ on the spaces 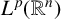$L^{p}(\mathbb {R}^{n})$ and 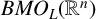$BMO_{L}(\mathbb {R}^{n})$, respectively. As extensions of $L^{p}(\mathbb {R}^{n})$, the boundedness of the operators 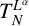$T_N^{L^{\alpha }}$ and $T^*_{L^{\alpha }}$ on the Morrey space $L^{\rho ,\theta }_{p,\kappa }(\mathbb {R}^{n})$ and the weak Morrey space $WL^{\rho ,\theta }_{1,\kappa }(\mathbb {R}^{n})$ has also been proved.

We prove that the uncentered Hardy–Littlewood maximal operator is discontinuous on ${BMO}(\mathbb {R}^n)$ and maps ${VMO}(\mathbb {R}^n)$ to itself. A counterexample to the boundedness of the strong and directional maximal operators on ${BMO}(\mathbb {R}^n)$ is given, and properties of slices of ${BMO}(\mathbb {R}^n)$ functions are discussed.

Our first result is a noncommutative form of the Jessen-Marcinkiewicz-Zygmund theorem for the maximal limit of multiparametric martingales or ergodic means. It implies bilateral almost uniform convergence (a noncommutative analogue of almost everywhere convergence) with initial data in the expected Orlicz spaces. A key ingredient is the introduction of the $L_p$ -norm of the $\limsup $ of a sequence of operators as a localized version of a $\ell _\infty /c_0$ -valued $L_p$ -space. In particular, our main result gives a strong $L_1$ -estimate for the $\limsup $ —as opposed to the usual weak $L_{1,\infty }$ -estimate for the $\mathop {\mathrm {sup}}\limits $ —with interesting consequences for the free group algebra.

Let $\mathcal{L} \mathbf{F} _2$ denote the free group algebra with $2$ generators, and consider the free Poisson semigroup generated by the usual length function. It is an open problem to determine the largest class inside $L_1(\mathcal{L} \mathbf{F} _2)$ for which the free Poisson semigroup converges to the initial data. Currently, the best known result is $L \log ^2 L(\mathcal{L} \mathbf{F} _2)$ . We improve this result by adding to it the operators in $L_1(\mathcal{L} \mathbf{F} _2)$ spanned by words without signs changes. Contrary to other related results in the literature, this set grows exponentially with length. The proof relies on our estimates for the noncommutative $\limsup $ together with new transference techniques.

We also establish a noncommutative form of Córdoba/Feffermann/Guzmán inequality for the strong maximal: more precisely, a weak $(\Phi ,\Phi )$ inequality—as opposed to weak $(\Phi ,1)$ —for noncommutative multiparametric martingales and $\Phi (s) = s (1 + \log _+ s)^{2 + \varepsilon }$ . This logarithmic power is an $\varepsilon $ -perturbation of the expected optimal one. The proof combines a refinement of Cuculescu’s construction with a quantum probabilistic interpretation of M. de Guzmán’s original argument. The commutative form of our argument gives the simplest known proof of this classical inequality. A few interesting consequences are derived for Cuculescu’s projections.

This paper is an attempt to understand a phenomenon of maximal operators associated with bases of three-dimensional rectangles of dimensions $(t,1/t,s)$ within a framework of more general Soria bases. The Jessen–Marcinkiewicz–Zygmund Theorem implies that the maximal operator associated with a Soria basis continuously maps $L\log^2L$ into $L^{1,\infty}$. We give a simple geometric condition that guarantees that the $L\log^2L$ class cannot be enlarged. The proof develops the author's methods applied previously in the two-dimensional case and is related to theorems of Córdoba, Soria and Fefferman and Pipher.

For a function $f\in L^p(\mathbb{R}d)$, $d\ge 2$, let $A_tf(x)$ be the mean of $f$ over the sphere of radius $t$ centred at $x$. Given a set $E\subset(0,\infty)$ of dilations we prove various endpoint bounds for the maximal operator $M_E$ defined by $M_E f(x)=\sup_{t\in E}|A_tf(x)|$, under some regularity assumptions on $E$.

AMS 2000 Mathematics subject classification: Primary 42B25. Secondary 42B20