We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
For any Liouville number 
$\alpha $, all of the following are transcendental numbers: 
${e}^\alpha $,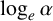 
$\log _{e}\alpha $, 
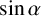$\sin \alpha $, 
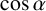$\cos \alpha $, 
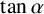$\tan \alpha $, 
$\sinh \alpha $,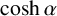 
$\cosh \alpha $, 
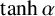$\tanh \alpha $, 
$\arcsin \alpha $ and the inverse functions evaluated at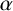 
$\alpha $ of the listed trigonometric and hyperbolic functions, noting that wherever multiple values are involved, every such value is transcendental. This remains true if ‘Liouville number’ is replaced by ‘U-number’, where U is one of Mahler’s classes of transcendental numbers.
