For $s\in [\tfrac {1}{2},\, 1)$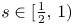 , let $u$
, let $u$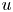 solve $(\partial _t - \Delta )^s u = Vu$
solve $(\partial _t - \Delta )^s u = Vu$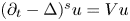 in $\mathbb {R}^{n} \times [-T,\, 0]$
in $\mathbb {R}^{n} \times [-T,\, 0]$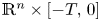 for some $T>0$
for some $T>0$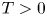 where $||V||_{ C^2(\mathbb {R}^n \times [-T, 0])} < \infty$
where $||V||_{ C^2(\mathbb {R}^n \times [-T, 0])} < \infty$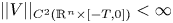 . We show that if for some $0<\mathfrak {K} < T$
. We show that if for some $0<\mathfrak {K} < T$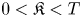 and $\epsilon >0$
and $\epsilon >0$
\[ {\unicode{x2A0D}}-_{[-\mathfrak{K},\, 0]} u^2(x, t) {\rm d}t \leq Ce^{-|x|^{2+\epsilon}}\ \forall x \in \mathbb{R}^n, \]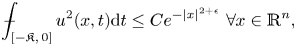
then $u \equiv 0$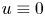 in $\mathbb {R}^{n} \times [-T,\, 0]$
in $\mathbb {R}^{n} \times [-T,\, 0]$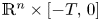 .
.