We give a simple expression for the joint probability density of: (a) the maximum value Y = max [X(t), 0 ≦ t ≦ T); (b) its location 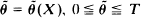 ; (c) the endpoint X(T), where X(t) = Xc(t) is a Wiener process with drift, Xc(t) = W(t) + ct, 0 ≦ t ≦ T. That is, we find the density p(θ, y, x) = p(θ, y, x; c, T) of
; (c) the endpoint X(T), where X(t) = Xc(t) is a Wiener process with drift, Xc(t) = W(t) + ct, 0 ≦ t ≦ T. That is, we find the density p(θ, y, x) = p(θ, y, x; c, T) of 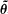 , Y, X(T), p(θ, y, x;
, Y, X(T), p(θ, y, x; 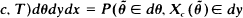 , Xc(T) ∈ dx) is given by, 0 < θ < T, x ≦ y, 0 < y,
, Xc(T) ∈ dx) is given by, 0 < θ < T, x ≦ y, 0 < y,
