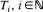1 results
A martingale approach to the PASTA property
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 30 / Issue 1 / March 1993
- Published online by Cambridge University Press:
- 14 July 2016, pp. 252-257
- Print publication:
- March 1993
-
- Article
- Export citation
-
It is known (Weizsäcker and Winkler (1990)) that for bounded predictable functions H and a Poisson process with jump times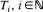
exists almost surely, and that in this case both limits are equal. Here we relax the boundedness condition on H. Our tool is a law of large numbers for local L2-martingales. We show by examples that our condition is close to optimal. Furthermore we indicate a generalization to point processes on more general spaces. The above property is called PASTA (‘Poisson arrivals see time averages') and is heavily used in queueing theory.
