We define and study jet bundles in the geometric orbifold category. We show that the usual arguments from the compact and the logarithmic settings do not all extend to this more general framework. This is illustrated by simple examples of orbifold pairs of general type that do not admit any global jet differential, even if some of these examples satisfy the Green–Griffiths–Lang conjecture. This contrasts with an important result of Demailly (Holomorphic Morse inequalities and the Green-Griffiths-Lang conjecture, Pure Appl. Math. Q. 7 (2011), 1165–1207) proving that compact varieties of general type always admit jet differentials. We illustrate the usefulness of the study of orbifold jets by establishing the hyperbolicity of some orbifold surfaces, that cannot be derived from the current techniques in Nevanlinna theory. We also conjecture that Demailly's theorem should hold for orbifold pairs with smooth boundary divisors under a certain natural multiplicity condition, and provide some evidence towards it.

This article establishes a sufficient condition for Kobayashi hyperbolicity of unbounded domains in terms of curvature. Specifically, when $\Omega \,\subset \,{{\mathbb{C}}^{n}}$ corresponds to a sub-level set of a smooth, real-valued function Ψ such that the form 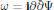$\omega \,=\,\mathbf{i}\partial \bar{\partial }\Psi $ is Kähler and has bounded curvature outside a bounded subset, then this domain admits a hermitian metric of strictly negative holomorphic sectional curvature.

We discuss a possible approach to the study of the vanishing of the Kobayashi pseudo-metric of a projective variety X, using chains of rational or elliptic curves contained in an arbitrarily small neighbourhood of X in projective space for the Euclidean topology.

Let n=2,3,4,5 and let X be a smooth complex projective hypersurface of . In this paper we find an effective lower bound for the degree of X, such that every holomorphic entire curve in X must satisfy an algebraic differential equation of order k=n=dim X, and also similar bounds for order k>n. Moreover, for every integer n≥2, we show that there are no such algebraic differential equations of order k<n for a smooth hypersurface in .