The existence of isometric embedding of $S_q^m$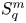 into $S_p^n$
into $S_p^n$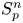 , where $1\leq p\neq q\leq \infty$
, where $1\leq p\neq q\leq \infty$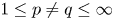 and $m,n\geq 2$
and $m,n\geq 2$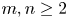 , has been recently studied in [6]. In this article, we extend the study of isometric embeddability beyond the above-mentioned range of $p$
, has been recently studied in [6]. In this article, we extend the study of isometric embeddability beyond the above-mentioned range of $p$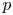 and $q$
and $q$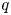 . More precisely, we show that there is no isometric embedding of the commutative quasi-Banach space $\ell _q^m(\mathbb {R})$
. More precisely, we show that there is no isometric embedding of the commutative quasi-Banach space $\ell _q^m(\mathbb {R})$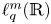 into $\ell _p^n(\mathbb {R})$
into $\ell _p^n(\mathbb {R})$ , where $(q,p)\in (0,\infty )\times (0,1)$
, where $(q,p)\in (0,\infty )\times (0,1)$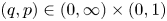 and $p\neq q$
and $p\neq q$ . As non-commutative quasi-Banach spaces, we show that there is no isometric embedding of $S_q^m$
. As non-commutative quasi-Banach spaces, we show that there is no isometric embedding of $S_q^m$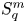 into $S_p^n$
into $S_p^n$ , where $(q,p)\in (0,2)\setminus \{1\}\times (0,1)$
, where $(q,p)\in (0,2)\setminus \{1\}\times (0,1)$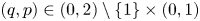 $\cup \, \{1\}\times (0,1)\setminus \left \{\!\frac {1}{n}:n\in \mathbb {N}\right \}$
$\cup \, \{1\}\times (0,1)\setminus \left \{\!\frac {1}{n}:n\in \mathbb {N}\right \}$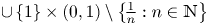 $\cup \, \{\infty \}\times (0,1)\setminus \left \{\!\frac {1}{n}:n\in \mathbb {N}\right \}$
$\cup \, \{\infty \}\times (0,1)\setminus \left \{\!\frac {1}{n}:n\in \mathbb {N}\right \}$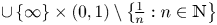 and $p\neq q$
and $p\neq q$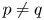 . Moreover, in some restrictive cases, we also show that there is no isometric embedding of $S_q^m$
. Moreover, in some restrictive cases, we also show that there is no isometric embedding of $S_q^m$ into $S_p^n$
into $S_p^n$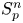 , where $(q,p)\in [2, \infty )\times (0,1)$
, where $(q,p)\in [2, \infty )\times (0,1)$ . A new tool in our paper is the non-commutative Clarkson's inequality for Schatten class operators. Other tools involved are the Kato–Rellich theorem and multiple operator integrals in perturbation theory, followed by intricate computations involving power-series analysis.
. A new tool in our paper is the non-commutative Clarkson's inequality for Schatten class operators. Other tools involved are the Kato–Rellich theorem and multiple operator integrals in perturbation theory, followed by intricate computations involving power-series analysis.
 into $S_p^n$
into $S_p^n$ as non-commutative quasi-Banach spaces
as non-commutative quasi-Banach spaces