Using the Dadarlat isomorphism, we give a characterization for the Kasparov product of  ${{C}^{*}}$-algebra extensions. A certain relation between
${{C}^{*}}$-algebra extensions. A certain relation between 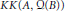 $KK\left( A,\,Q\left( B \right) \right)$ and
$KK\left( A,\,Q\left( B \right) \right)$ and 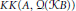 $KK\left( A,\,Q\left( KB \right) \right)$ is also considered when
$KK\left( A,\,Q\left( KB \right) \right)$ is also considered when  $B$ is not stable, and it is proved that
$B$ is not stable, and it is proved that 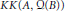 $KK\left( A,\,Q\left( B \right) \right)$ and
$KK\left( A,\,Q\left( B \right) \right)$ and 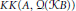 $KK\left( A,\,Q\left( KB \right) \right)$ are not isomorphic in general.
$KK\left( A,\,Q\left( KB \right) \right)$ are not isomorphic in general.