This paper is a continuation of the paper, Matsumoto [‘Subshifts, $\lambda $ -graph bisystems and $C^*$ -algebras’, J. Math. Anal. Appl. 485 (2020), 123843]. A $\lambda $ -graph bisystem consists of a pair of two labeled Bratteli diagrams satisfying a certain compatibility condition on their edge labeling. For any two-sided subshift $\Lambda $ , there exists a $\lambda $ -graph bisystem satisfying a special property called the follower–predecessor compatibility condition. We construct an AF-algebra ${\mathcal {F}}_{\mathcal {L}}$ with shift automorphism $\rho _{\mathcal {L}}$ from a $\lambda $ -graph bisystem $({\mathcal {L}}^-,{\mathcal {L}}^+)$ , and define a $C^*$ -algebra ${\mathcal R}_{\mathcal {L}}$ by the crossed product . It is a two-sided subshift analogue of asymptotic Ruelle algebras constructed from Smale spaces. If $\lambda $ -graph bisystems come from two-sided subshifts, these $C^*$ -algebras are proved to be invariant under topological conjugacy of the underlying subshifts. We present a simplicity condition of the $C^*$ -algebra ${\mathcal R}_{\mathcal {L}}$ and the K-theory formulas of the $C^*$ -algebras ${\mathcal {F}}_{\mathcal {L}}$ and ${\mathcal R}_{\mathcal {L}}$ . The K-group for the AF-algebra ${\mathcal {F}}_{\mathcal {L}}$ is regarded as a two-sided extension of the dimension group of subshifts.

A connected space is called a C0-space if its rational cup product is trivial. A characterizing property of C0-spaces is obtained. This property is used to calculate the algebraic K0-group K0(C𝔽(X)) of the ring of continuous functions for infinite-dimensional complexes X.

We prove that the K-group of reciprocity functors, defined by F. Ivorra and the first author, vanishes over a perfect field as soon as one of the reciprocity functors is and one is an abelian variety.

Let p be an odd prime and L/F a p-extension of number fields with Galois group G. The aim of this paper is to provide answers to a question of Kahn concerning lower bounds for the order of the kernel and cokernel of the functorial map K2F → K2LG. To this end, we first determine a norm index formula for generalized Tate kernels and then express our lower bounds in terms of the ramification in L/F.

Let $A$ be an 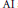$\text{AI}$ algebra; that is, $A$ is the 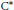${{\text{C}}^{*}}$-algebra inductive limit of a sequence

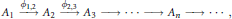$${{A}_{1}}\xrightarrow{{{\phi }_{1,2}}}{{A}_{2}}\xrightarrow{{{\phi }_{2,3}}}{{A}_{3}}\to \cdot \cdot \cdot \to {{A}_{n}}\to \cdot \cdot \cdot ,$$

where 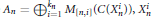${{A}_{n}}=\oplus _{i=1}^{{{k}_{n}}}{{M}_{\left[ n,i \right]}}\left( C\left( X_{n}^{i} \right) \right),X_{n}^{i}$ are [0, 1], ${{k}_{n}}$, and 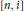$\left[ n,\,i \right]$ are positive integers. Suppose that $A$ has the ideal property: each closed two-sided ideal of $A$ is generated by the projections inside the ideal, as a closed two-sided ideal. In this article, we give a complete classification of 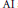$\text{AI}$ algebras with the ideal property.